2025年新课程学习与检测九年级数学上册
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年新课程学习与检测九年级数学上册 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第46页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
9. 下列四组三角形中,是相似三角形的一组是 (

A
)
答案:
9.A
10. 如图所示,$\triangle ABC\backsim\triangle ADB$,$AD=1$,$AB=2$,则AC的长为 (
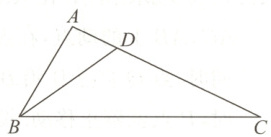
A.$\sqrt{2}$
B.2
C.3
D.4
D
)
A.$\sqrt{2}$
B.2
C.3
D.4
答案:
10.D
11. 已知$\frac{x}{y}=\frac{3}{4}$,则$\frac{2x-y}{x+y}=$
$\frac{2}{7}$
.
答案:
11.$\frac{2}{7}$
12. 如图所示,五边形ABCDE与五边形$A'B'C'D'E'$相似,且周长之比为$3:4$.若$CD=12$,则$C'D'$的长为
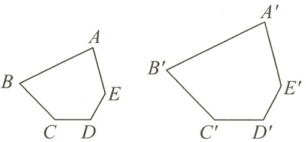
16
.
答案:
12.16
13. 在平面直角坐标系中有两点$A(4,0)$,$B(0,2)$,如果点C在x轴上(点C与点A不重合),当点C的坐标为
(−1,0)或(1,0)
时,$\triangle BOC\backsim\triangle AOB$.
答案:
13.(−1,0)或(1,0)
14. 《周髀算经》中记载了“偃矩以望高”的方法.“矩”在古代指两条边呈直角的曲尺(即图中的ABC).“偃矩以望高”的意思是把“矩”仰立放,可测量物体的高度.如图所示,点A,B,Q在同一水平线上,$\angle ABC$和$\angle AQP$均为直角,AP与BC相交于点D.测得$AB=0.4$ m,$BD=0.2$ m,$AQ=12$ m,则树高$PQ=$
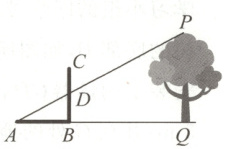
6
m.
答案:
14.6
15. 已知$\triangle ABC$与$\triangle A'B'C'$的相似比为$\frac{2}{3}$,且$S_{\triangle ABC}+S_{\triangle A'B'C'}=91$,则$\triangle A'B'C'$的面积是
63
.
答案:
15.63
16. (6分)已知$\frac{x}{3}=\frac{y}{4}=\frac{z}{6}$,且$2x+3y+z=6$,求$x+y-z$的值.
答案:
解:设$\frac{x}{3}=\frac{y}{4}=\frac{z}{6}=k$,则$x = 3k$,$y = 4k$,$z = 6k$。
因为$2x + 3y + z = 6$,所以$2×3k + 3×4k + 6k = 6$,
即$6k + 12k + 6k = 6$,
$24k = 6$,
解得$k=\frac{1}{4}$。
所以$x = 3×\frac{1}{4}=\frac{3}{4}$,$y = 4×\frac{1}{4} = 1$,$z = 6×\frac{1}{4}=\frac{3}{2}$。
则$x + y - z=\frac{3}{4}+1-\frac{3}{2}$
$=\frac{3}{4}+1-\frac{6}{4}$
$=\frac{3 + 4 - 6}{4}$
$=\frac{1}{4}$。
综上,$x + y - z$的值为$\frac{1}{4}$。
因为$2x + 3y + z = 6$,所以$2×3k + 3×4k + 6k = 6$,
即$6k + 12k + 6k = 6$,
$24k = 6$,
解得$k=\frac{1}{4}$。
所以$x = 3×\frac{1}{4}=\frac{3}{4}$,$y = 4×\frac{1}{4} = 1$,$z = 6×\frac{1}{4}=\frac{3}{2}$。
则$x + y - z=\frac{3}{4}+1-\frac{3}{2}$
$=\frac{3}{4}+1-\frac{6}{4}$
$=\frac{3 + 4 - 6}{4}$
$=\frac{1}{4}$。
综上,$x + y - z$的值为$\frac{1}{4}$。
查看更多完整答案,请扫码查看


