《2025年新课程学习与检测九年级数学上册》

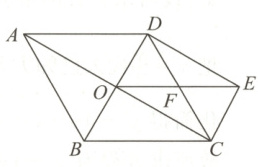
22. (10分)如图所示,在菱形$ABCD$中,对角线$AC$,$BD$相交于点$O$,$F$是$CD$的中点,延长$OF$到点$E$,使$EF = OF$,连接$CE$,$DE$.
(1)求证:四边形$DOCE$是矩形.
(2)若$OE = 4$,$\angle ABC = 120^{\circ}$,求菱形$ABCD$的面积.

答案： 22.
(1)证明:
∵F是CD的中点，
∴CF=DF.
∵OF=EF，
∴四边形DOCE是平行四边形.
∵四边形ABCD是菱形，
∴AC⊥BD，即∠DOC=90°.
∴四边形DOCE是矩形.
(2)解:
∵OE=4，四边形DOCE是矩形，
∴CD=OE=4.
∵四边形ABCD是菱形，
∴BD=2OB，AB=BC=CD=4，AC=2OC，AC⊥BD.
∴∠CBO=$\frac{1}{2} $∠ABC=60°.
∴∠BCO=90°-∠CBO=30°.
∴OB=$\frac{1}{2} $BC=2，OC=$\sqrt{BC^{2}-OB^{2}} $=$2\sqrt{3} $.
∴BD=2OB=4，AC=2OC=$4\sqrt{3} $.
∴四边形ABCD的面积为$\frac{1}{2} $BD·AC=$8\sqrt{3} $.

23. (10分)某商场举行促销活动,消费满一定金额的顾客可以通过参与摸球活动获得奖励.具体方法如下:从一个装有2个红球、3个黄球(仅颜色不同)的袋中摸出2个球,根据摸到的红球数确定奖励金额,具体金额设置如下表所示.

现有两种摸球方案:
方案一:随机摸出1个球,记下颜色后不放回,再从中随机摸出1个球.
方案二:随机摸出1个球,记下颜色后放回,再从中随机摸出1个球.
(1)求方案一中两次都摸到红球的概率.
(2)请你从平均收益的角度帮助顾客分析:选择哪种摸球方案更有利?

答案： 23.解:
(1)列表如下：
第二次 第一次 红1 红2 黄1 黄2 黄3
红1 — (红2,红1) (黄1,红1) (黄2,红1) (黄3,红1)
红2 (红1,红2) — (黄1,红2) (黄2,红2) (黄3,红2)
黄1 (红1,黄1) (红2,黄1) — (黄2,黄1) (黄3,黄1)
黄2 (红1,黄2) (红2,黄2) (黄1,黄2) (黄2,黄2) (黄3,黄2)
黄3 (红1,黄3) (红2,黄3) (黄1,黄3) (黄2,黄3) —
由表知，共有20种等可能的结果，其中两次都摸到红球的结果有2种，
∴两次都摸到红球的概率为$\frac{2}{20} =\frac{1}{10} $.
(2)由
(1)知，方案一的摸球方案的平均收益为$5×\frac{6}{20} +10×\frac{12}{20} +20×\frac{2}{20} =9.5$(元).
方案二摸球方式的所有结果列表如下：
红1 红2 黄1 黄2 黄3
红1 (红1,红1) (红2,红1) (黄1,红1) (黄2,红1) (黄3,红1)
红2 (红1,红2) (红2,红2) (黄1,红2) (黄2,红2) (黄3,红2)
黄1 (红1,黄1) (红2,黄1) (黄1,黄1) (黄2,黄1) (黄3,黄1)
黄2 (红1,黄2) (红2,黄2) (黄1,黄2) (黄2,黄2) (黄3,黄2)
黄3 (红1,黄3) (红2,黄3) (黄1,黄3) (黄2,黄3) (黄3,黄3)
由表知，共有25种等可能的结果，
∴方案二的摸球方案的平均收益为$5×\frac{9}{25} +10×\frac{12}{25} +20×\frac{4}{25} =9.8$(元).
∵9.8＞9.5，
∴方案二的摸球方式更有利.