2025年新课程学习与检测九年级数学上册
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年新课程学习与检测九年级数学上册 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第26页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
8. 如图所示,在矩形$ABCD$中,连接$BD$,将$\triangle BCD$沿对角线$BD$折叠得到$\triangle BDE$,$BE$交$AD$于点$O$,$BE$恰好平分$\angle ABD$. 若$AB = 2\sqrt{3}$,则点$O$到$BD$的距离为 (
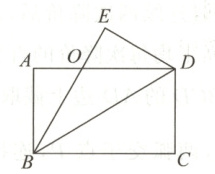
A.$\sqrt{3}$
B.2
C.$\frac{3}{2}\sqrt{3}$
D.3
B
)
A.$\sqrt{3}$
B.2
C.$\frac{3}{2}\sqrt{3}$
D.3
答案:
8.B
9. 甲、乙两名同学在一次用频率估计概率的试验中,统计了某一结果出现的频率,绘出的统计图如图所示,则符合这结果的试验可能是 (
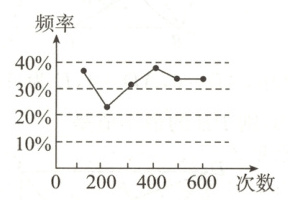
A.从一个装有2个白球和1个红球的袋子中任取1个球,取到红球的概率
B.任意买一张电影票,座位号是偶数的概率
C.抛一枚质地均匀的硬币,正面朝上的概率
D.掷一枚正六面体的骰子,出现1点的概率
A
)
A.从一个装有2个白球和1个红球的袋子中任取1个球,取到红球的概率
B.任意买一张电影票,座位号是偶数的概率
C.抛一枚质地均匀的硬币,正面朝上的概率
D.掷一枚正六面体的骰子,出现1点的概率
答案:
9.A
10. 如图所示,在菱形$ABCD$中,$\angle A = 60^{\circ}$,$E$,$F$分别是$AB$,$AD$的中点,$DE$,$BF$相交于点$G$,连接$BD$,$CG$. 下列结论正确的有 (
①$\angle FGE = 120^{\circ}$ ②$BG + DG = CG$ ③$\triangle BDF≌\triangle CGB$ ④$S_{四边形AEGF} = S_{\triangle BDG}$
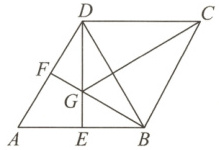
A.1个
B.2个
C.3个
D.4个
C
)①$\angle FGE = 120^{\circ}$ ②$BG + DG = CG$ ③$\triangle BDF≌\triangle CGB$ ④$S_{四边形AEGF} = S_{\triangle BDG}$

A.1个
B.2个
C.3个
D.4个
答案:
10.C 解析:$\because$四边形ABCD是菱形,
$\therefore AB=BC=CD=AD,\angle A=\angle BCD$。
$\because\angle A=60^{\circ}$,
$\therefore\angle BCD=60^{\circ},\triangle ABD$是等边三角形。
$\therefore\triangle BDC$是等边三角形,$\angle ADB=\angle ABD=60^{\circ}$。
$\therefore\angle CDB=\angle CBD=60^{\circ}$。
$\because E,F$分别是AB,AD的中点,
$\therefore\angle BFD=\angle DEB=90^{\circ}$。
$\therefore\angle GDB=\angle GBD=30^{\circ}$。
$\therefore\angle GDC=\angle GBC=90^{\circ},DG=BG$。
$\therefore\angle FGE=\angle BGD=360^{\circ}-90^{\circ}-90^{\circ}-60^{\circ}=120^{\circ}$,故①正确。
在$\triangle CDG$和$\triangle CBG$中,$\begin{cases}CD=CB, \\DG=BG, \\CG=CG,\end{cases}$
$\therefore\triangle CDG\cong\triangle CBG(SSS)$。
$\therefore\angle DGC=\angle BGC=60^{\circ}$,$\therefore\angle GCD=30^{\circ}$。
$\therefore CG=2GD=GD+GD$,故②正确。
$\because\triangle GBC$为直角三角形,
$\therefore CG>BC$,$\therefore CG\neq BD$。
$\therefore\triangle BDF$与$\triangle CGB$不全等,故③错误。
$\because\triangle ABC$是等边三角形,E,F分别是AB,AD的中点,
$\therefore S_{\triangle ADE}=S_{\triangle BDE}=S_{\triangle ABF}$。
$\therefore S_{\triangle DFG}=S_{\triangle BEG}$。
$\therefore S_{四边形AEGF}=S_{\triangle BDG}$,故④正确。
正确的有①②④,共3个,故选C。
$\therefore AB=BC=CD=AD,\angle A=\angle BCD$。
$\because\angle A=60^{\circ}$,
$\therefore\angle BCD=60^{\circ},\triangle ABD$是等边三角形。
$\therefore\triangle BDC$是等边三角形,$\angle ADB=\angle ABD=60^{\circ}$。
$\therefore\angle CDB=\angle CBD=60^{\circ}$。
$\because E,F$分别是AB,AD的中点,
$\therefore\angle BFD=\angle DEB=90^{\circ}$。
$\therefore\angle GDB=\angle GBD=30^{\circ}$。
$\therefore\angle GDC=\angle GBC=90^{\circ},DG=BG$。
$\therefore\angle FGE=\angle BGD=360^{\circ}-90^{\circ}-90^{\circ}-60^{\circ}=120^{\circ}$,故①正确。
在$\triangle CDG$和$\triangle CBG$中,$\begin{cases}CD=CB, \\DG=BG, \\CG=CG,\end{cases}$
$\therefore\triangle CDG\cong\triangle CBG(SSS)$。
$\therefore\angle DGC=\angle BGC=60^{\circ}$,$\therefore\angle GCD=30^{\circ}$。
$\therefore CG=2GD=GD+GD$,故②正确。
$\because\triangle GBC$为直角三角形,
$\therefore CG>BC$,$\therefore CG\neq BD$。
$\therefore\triangle BDF$与$\triangle CGB$不全等,故③错误。
$\because\triangle ABC$是等边三角形,E,F分别是AB,AD的中点,
$\therefore S_{\triangle ADE}=S_{\triangle BDE}=S_{\triangle ABF}$。
$\therefore S_{\triangle DFG}=S_{\triangle BEG}$。
$\therefore S_{四边形AEGF}=S_{\triangle BDG}$,故④正确。
正确的有①②④,共3个,故选C。
11. 某林业部门为了调查某种幼树在一定条件下的移植成活率,在同等条件下,对这种幼树进行大量移植,并统计成活情况,下表是这种幼树移植过程中的一组统计数据:

估计该种幼树在此条件下移植成活的概率是

估计该种幼树在此条件下移植成活的概率是
0.9
. (结果精确到0.1)
答案:
11.0.9
查看更多完整答案,请扫码查看


