2025年新课程学习与检测九年级数学上册
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年新课程学习与检测九年级数学上册 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第34页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
8. 某小区内的一家快递驿站第一天共收到225件快递,第三天共收到324件快递,设该快递驿站收件量的日平均增长率为$x$,则下列方程正确的是 (
A.$225(1 + x^2) = 324$
B.$225(1 + x)^2 = 324$
C.$225(1 + 2x) = 324$
D.$225 + 225(1 + x) = 324$
B
)A.$225(1 + x^2) = 324$
B.$225(1 + x)^2 = 324$
C.$225(1 + 2x) = 324$
D.$225 + 225(1 + x) = 324$
答案:
8.B
9. 某小组做“用频率估计概率”的试验时,统计了某一事件发生的频率,绘制了折线图,如图所示.该事件最有可能是 (
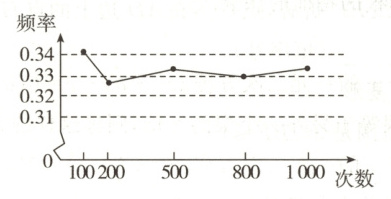
A.掷一个质地均匀的正六面骰子,向上一面的点数是2
B.从一副扑克牌中任意抽取1张,这张牌是“红心”
C.暗箱中有1个红球和2个黄球,这些球除了颜色外无其他差别,从中任取1个球是红球
D.掷一枚硬币,正面朝上
C
)
A.掷一个质地均匀的正六面骰子,向上一面的点数是2
B.从一副扑克牌中任意抽取1张,这张牌是“红心”
C.暗箱中有1个红球和2个黄球,这些球除了颜色外无其他差别,从中任取1个球是红球
D.掷一枚硬币,正面朝上
答案:
9.C
10. 如图所示,在矩形$ABCD$中,$AB = 1$,$BC = 2$,$E$是边$BC$上一动点,$F$是对角线$BD$上一动点,且$BE = DF$,则$DE + CF$的最小值为 (
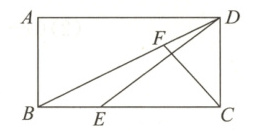
A.3
B.$2\sqrt{3}$
C.$\sqrt{5}$
D.$\sqrt{6}$
D
)
A.3
B.$2\sqrt{3}$
C.$\sqrt{5}$
D.$\sqrt{6}$
答案:
10.D 解析:如图所示,延长DA到点G,使DG=DB,连接FG,CG.

∵四边形ABCD是矩形,
∴AD//BC,AD=BC=2,DC=AB=1,∠BAD=∠GDC=90°.
∴∠GDF=∠DBE.
∵DF=BE,DG=BD,
∴△DGF≌△BDE(SAS).
∴FG=DE.
∴DE+CF=FG+CF.
∴当点G,F,C共线时,FG+CF最小,最小值为CG的长.
∵∠BAD=90°,
∴BD=$\sqrt{AB^{2}+AD^{2}} $=$\sqrt{1^{2}+2^{2}} $=$\sqrt{5} $.
在Rt△GDC中,GD=BD=$\sqrt{5} $,∠GDC=90°,
∴CG=$\sqrt{CD^{2}+DG^{2}} $=$\sqrt{1+5} $=$\sqrt{6} $.
∴DE+CF的最小值为$\sqrt{6} $.故选D.
10.D 解析:如图所示,延长DA到点G,使DG=DB,连接FG,CG.

∵四边形ABCD是矩形,
∴AD//BC,AD=BC=2,DC=AB=1,∠BAD=∠GDC=90°.
∴∠GDF=∠DBE.
∵DF=BE,DG=BD,
∴△DGF≌△BDE(SAS).
∴FG=DE.
∴DE+CF=FG+CF.
∴当点G,F,C共线时,FG+CF最小,最小值为CG的长.
∵∠BAD=90°,
∴BD=$\sqrt{AB^{2}+AD^{2}} $=$\sqrt{1^{2}+2^{2}} $=$\sqrt{5} $.
在Rt△GDC中,GD=BD=$\sqrt{5} $,∠GDC=90°,
∴CG=$\sqrt{CD^{2}+DG^{2}} $=$\sqrt{1+5} $=$\sqrt{6} $.
∴DE+CF的最小值为$\sqrt{6} $.故选D.
11. 若$x = 2$是一元二次方程$ax^2 - 4x + 1 = 0$的一个根,则$a$的值是
$\frac{7}{4}$
.
答案:
11.$\frac{7}{4}$
12. 如图所示,在$\triangle ABC$中,$AB = AC$,点$D$在$BC$边上,$DF // AB$,$DE // AC$,则当$\angle B =$
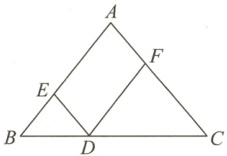
45
$^{\circ}$时,四边形$AEDF$是矩形.
答案:
12.45
13. 若$a$,$b$是互不相等的两个实数,且分别满足$a^2 - a - 1 = 0$,$b^2 - b - 1 = 0$,则$a + b + 2ab =$
-1
.
答案:
13.−1
14. 如图所示,在$□ ABCD$中,$AB = 3$,$AD = 4$,以点$A$为圆心,$AB$长为半径画弧,交$AD$于点$F$,再分别以点$B$,$F$为圆心,大于$\frac{1}{2}BF$的长为半径画弧,两弧交于点$P$,连接$AP$并延长,交$BC$于点$E$,连接$EF$,则四边形$ECDF$的周长为
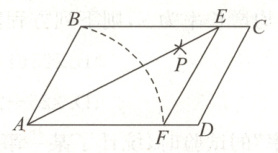
8
.
答案:
14.8
查看更多完整答案,请扫码查看


