《2025年新课程学习与检测九年级数学上册》

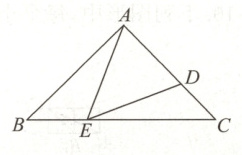
18. (6分) 如图所示, 在 $ Rt \triangle ABC $ 中, $ \angle BAC = 90° $, $ AB = AC $, $ E $, $ D $ 分别是 $ BC $, $ AC $ 上的点, 且 $ \angle AED = 45° $. 求证: $ \triangle ABE \sim \triangle ECD $.

答案： 18.证明:
∵∠BAC = 90°,AB = AC,
∴∠B = ∠C = 45°.
∵∠AEC = ∠B + ∠BAE,
∴∠AED + ∠CED = ∠B + ∠BAE.
　又
∵∠AED = 45°,
∴∠BAE = ∠CED.
∴△ABE∽△ECD.

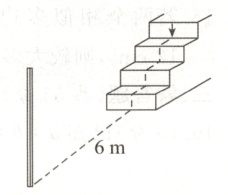
19. (6分) 在一个阶梯旁 $ 6 \, m $ 的地方立有 $ 1 $ 根柱子, 其影子的前端正好到达阶梯前第 $ 3 $ 阶(箭头). 另外, 此时树立 $ 1 $ 根长 $ 70 \, cm $ 的竹竿, 其影子的长度为 $ 175 \, cm $. 设阶梯各阶的高度与深度都是 $ 50 \, cm $, 求柱子的高度.

答案： 19.解:6m = 600cm,
　设柱子的高度为xcm,
　则(600 + 50×3):(x - 150) = 175:70,
即175(x - 150) = 750×70,
　　解得x = 450.
　　经检验，x = 450是方程的根.
　　答:柱子的高度是450cm.

20. (6分) 如图所示, $ BD // AC $, $ AB $ 与 $ CD $ 相交于点 $ O $, 已知 $ \triangle OBD \sim \triangle OAC $, $ \frac{OD}{OC} = \frac{2}{3} $, $ OB = 2 $, 求 $ AB $ 的长.

答案： 20.解:
∵△OBD∽△OAC,
∴$\frac{OB}{OA}=\frac{OD}{OC}=\frac{2}{3}$.
∵$\frac{2}{OA}=\frac{2}{3}$,解得OA = 3.
∴AB = OA + OB = 3 + 2 = 5.