《2025年新课程学习与检测九年级数学上册》

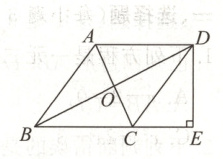
21. (8 分) 如图所示, $O$ 为 $\triangle ABC$ 的边 $AC$ 的中点, $AD// BC$, 交 $BO$ 的延长线于点 $D$, 连接 $DC$, $DB$ 平分 $\angle ADC$, 作 $DE\perp BC$, 垂足为 $E$.
(1) 求证: 四边形 $ABCD$ 为菱形.
(2) 若 $BD = 8$, $AC = 6$, 求 $DE$ 的长.

答案：
(1)证明：$\because O$为$\triangle ABC$的边$AC$的中点，
$AD// BC$,
$\therefore OA = OC,\angle OAD = \angle OCB,\angle ADB = \angle CBD$.
在$\triangle OAD$和$\triangle OCB$中，
$\begin{cases}\angle OAD = \angle OCB,\\OA = OC,\\\angle AOD = \angle COB,\end{cases}$
$\therefore\triangle OAD\cong\triangle OCB(ASA)$.
$\therefore OD = OB$.
$\therefore$四边形$ABCD$是平行四边形.
$\because DB$平分$\angle ADC$,$\therefore\angle ADB = \angle CDB$.
$\therefore\angle CBD = \angle CDB.\therefore BC = DC$.
$\therefore$四边形$ABCD$是菱形.
(2)解：$\because$四边形$ABCD$是菱形，
$\therefore OB = \frac{1}{2}BD = 4,OC = \frac{1}{2}AC = 3$,
$AC\perp BD$.
$\therefore\angle BOC = 90^{\circ}$.
$\therefore BC = \sqrt{OB^{2}+OC^{2}} = 5$.
$\because DE\perp BC$,$\therefore\angle E = 90^{\circ}=\angle BOC$.
$\because\angle OBC = \angle EBD$,$\therefore\triangle BOC\sim\triangle BED$.
$\therefore\frac{CO}{DE} = \frac{BC}{BD}$,即$\frac{3}{DE} = \frac{5}{8}$,解得$DE = \frac{24}{5}$.

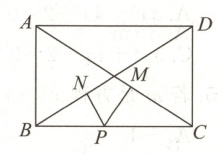
22. (8 分) 如图所示, 在矩形 $ABCD$ 中, $AB = 30$, $AD = 40$, $P$ 为 $BC$ 上的一个动点, 过点 $P$ 作 $PM\perp AC$ 于点 $M$, $PN\perp BD$ 于点 $N$, 当点 $P$ 在 $BC$ 上运动时, $PM + PN$ 的值是否发生变化? 若不变, 请求出定值.

答案： 解：当点$P$在$BC$上运动时，$PM + PN$的值不发生变化，
理由：设$AC$与$BD$交于点$O$,连接$PO$,图略.
$\because$在矩形$ABCD$中，$AB = 30,BC = AD = 40$,
$\therefore AC = BD,\angle ABC = 90^{\circ},AO = OC = BO = OD$.
由勾股定理得$AC = 50$,
$\therefore AO = OC = OB = OD = 25$.
$\therefore S_{\triangle ABC} = \frac{1}{2}AB× BC = \frac{1}{2}×30×40 = 600$.
$\therefore S_{\triangle BOC} = \frac{1}{2}S_{\triangle ABC} = 300$.
$\therefore\frac{1}{2}× BO× PN + \frac{1}{2}× CO× PM = 300$.
$\therefore PM + PN = 24$.
即当点$P$在$BC$上运动时，$PM + PN$的值不发生变化，永远是$24$.

23. (12 分) 如图所示, 四边形 $ABCD$ 和 $CGEF$ 都是正方形, $M$ 是 $AE$ 的中点.

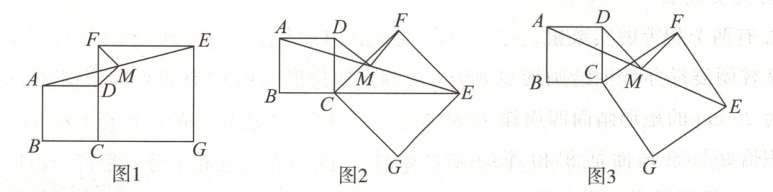
(1) 如图 1 所示, 点 $G$ 在 $BC$ 的延长线上, 求证: $DM = MF$.
(2) 在图 1 的基础上, 将正方形 $CGEF$ 绕点 $C$ 按顺时针方向旋转到图 2 的位置, 此时点 $E$ 在 $BC$ 的延长线上. 求证: $DM = MF$.
(3) 在图 2 的基础上, 将正方形 $CGEF$ 绕点 $C$ 再任意旋转一个角度到图 3 的位置, 此时 $DM$ 和 $MF$ 还相等吗? (不必说明理由)

答案：

(1)证明：延长$DM$,交$FE$于点$N$,如图1所示.
$\because$四边形$ABCD,CGEF$都是正方形，
$\therefore CF = EF,AD = DC,\angle CFE = 90^{\circ}$,
$AD// FE$.
$\therefore\angle MAD = \angle NEM$.
又$\because MA = ME,\angle AMD = \angle NME$,
$\therefore\triangle AMD\cong\triangle EMN$.
$\therefore DM = MN$.
$\therefore M$为直角三角形$DFN$的中点.
$\therefore 2FM = DN.\therefore MF = MD$.

(2)证明：延长$DM$到点$N$,使$MN = MD$,
连接$FD,FN,EN$,
延长$EN$,与直线$DC$交于点$H$,如图2所示.
$\because MA = ME,\angle AMD = \angle EMN,MD = MN$,
$\therefore\triangle AMD\cong\triangle EMN$.
$\therefore\angle DAM = \angle MEN,AD = NE$.
又$\because$四边形$ABCD,CGEF$为正方形，
$\therefore CF = EF,AD = DC,\angle ADC = 90^{\circ}$,
$\angle CFE = \angle ADC = \angle FEG = \angle FCG = 90^{\circ}$.
$\therefore DC = NE$.
$\because\angle DAM = \angle MEN$,$\therefore AD// EH$.
$\therefore\angle H = \angle ADC = 90^{\circ}.\therefore$点$H$与点$C$重合.
$\because\angle FEC = \angle FCE = 45^{\circ}$,
$\therefore\angle DCF = 45^{\circ}$.
$\therefore\angle DCF = \angle FEN$.
又$\because FC = FE,DC = EN$,
$\therefore\triangle DCF\cong\triangle NEF$.
$\therefore FD = FN,\angle DFC = \angle NFE$.
$\because\angle CFE = 90^{\circ}$,$\therefore\angle DFN = 90^{\circ}$.
$\therefore FM\perp MD,MF = MD$.

(3)相等.