2025年新课程学习与检测九年级数学上册
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年新课程学习与检测九年级数学上册 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第20页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
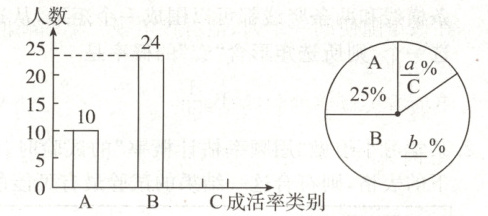
20. (8 分) 某校张老师为了解本班学生 3 月植树的成活情况, 对本班全体学生进行了调查, 并将调查结果分为三类: A. 好; B. 中; C. 差. 请根据图中信息, 解答下列问题.
(1) 求全班学生总人数.
(2) 在扇形统计图中, $ a = $
(3) 张老师在班上随机抽取了 4 名学生, 其中 A 类 1 人, B 类 2 人, C 类 1 人, 若再从这 4 人中随机抽取 2 人, 求出全是 B 类学生的概率.
(1) 求全班学生总人数.
(2) 在扇形统计图中, $ a = $
15
, $ b = $60
, C 类的圆心角为54°
.(3) 张老师在班上随机抽取了 4 名学生, 其中 A 类 1 人, B 类 2 人, C 类 1 人, 若再从这 4 人中随机抽取 2 人, 求出全是 B 类学生的概率.

答案:
20.
(1)解:全班学生总人数为10÷25% = 40.
(2)15 60 54° 解析:
∵C类人数为40 - (10 + 24) = 6,
∴C类所占百分比为$\frac{6}{40}$×100% = 15%,
C类的圆心角为360°×$\frac{6}{40}$ = 54°,
B类所占百分比为$\frac{24}{40}$×100% = 60%,
∴a = 15,b = 60,C类的圆心角为54°.
(3)解:列表,如下表所示.
第二次 第一次抽取
抽取 A B B C
A — BA BA CA
B AB — BB CB
B AB BB — CB
C AC BC BC —
由表可知,共有12种等可能的结果,其中全是B类学生的结果有2种,
∴全是B类学生的概率为$\frac{2}{12}$=$\frac{1}{6}$.
(1)解:全班学生总人数为10÷25% = 40.
(2)15 60 54° 解析:
∵C类人数为40 - (10 + 24) = 6,
∴C类所占百分比为$\frac{6}{40}$×100% = 15%,
C类的圆心角为360°×$\frac{6}{40}$ = 54°,
B类所占百分比为$\frac{24}{40}$×100% = 60%,
∴a = 15,b = 60,C类的圆心角为54°.
(3)解:列表,如下表所示.
第二次 第一次抽取
抽取 A B B C
A — BA BA CA
B AB — BB CB
B AB BB — CB
C AC BC BC —
由表可知,共有12种等可能的结果,其中全是B类学生的结果有2种,
∴全是B类学生的概率为$\frac{2}{12}$=$\frac{1}{6}$.
21. (8 分) 某校组织学生去展览馆看展览, 该展览馆有 2 个验票口 A,B(可进出), 另外还有 2 个出口C,D(不许进). 小张同学凭票进入展览大厅, 参观结束后离开.

(1) 小张从进入到离开共有多少种可能的进出方式? (要求用树状图法或列表法表示)
(2) 小张不从同一个验票口进出的概率是多少?

(1) 小张从进入到离开共有多少种可能的进出方式? (要求用树状图法或列表法表示)
(2) 小张不从同一个验票口进出的概率是多少?
答案:
21.解:
(1)画树状图,如图所示.

则小张从进入到离开共有8种可能的进出方式.
(2)
∵小张不从同一个验票口进出的情况有6种,
∴P(小张不从同一个验票口进出)=$\frac{6}{8}$=$\frac{3}{4}$.
21.解:
(1)画树状图,如图所示.

则小张从进入到离开共有8种可能的进出方式.
(2)
∵小张不从同一个验票口进出的情况有6种,
∴P(小张不从同一个验票口进出)=$\frac{6}{8}$=$\frac{3}{4}$.
22. (12 分) 如图所示, 用两个转盘进行“配紫色”游戏, 规则如下: 游戏者转动两个转盘各转一次, 转盘停止后, 如果两个指针所在的区域的颜色是一红一蓝, 就说“配成紫色”, 则游戏者获胜.
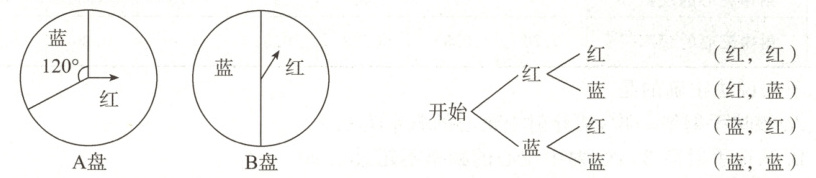
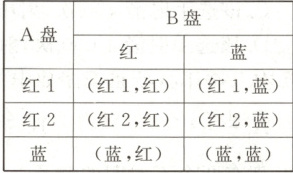
小颖制作了树状图, 并据此求出游戏者获胜的概率为 $\frac{1}{2}$; 小亮则先把左边转盘的红色区域等分成 2 份, 分别记作“红 1”“红 2”, 然后制作了表格, 据此求出游戏者获胜的概率也是 $\frac{1}{2}$.
(1) 你认为谁做得对? 说说你的理由.
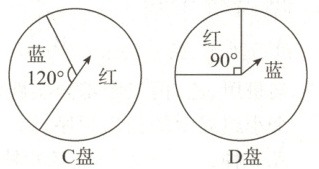
(2) 将转盘改为如图所示的转盘, 请求出“配成紫色”的概率, 请以这两题为例, 说说将非等可能事件转化为等可能事件的关键是什么.


小颖制作了树状图, 并据此求出游戏者获胜的概率为 $\frac{1}{2}$; 小亮则先把左边转盘的红色区域等分成 2 份, 分别记作“红 1”“红 2”, 然后制作了表格, 据此求出游戏者获胜的概率也是 $\frac{1}{2}$.
(1) 你认为谁做得对? 说说你的理由.
(2) 将转盘改为如图所示的转盘, 请求出“配成紫色”的概率, 请以这两题为例, 说说将非等可能事件转化为等可能事件的关键是什么.

答案:
22.解:
(1)小颖的做法不正确,小亮的做法正确.
理由:
∵左边的转盘中红色部分和蓝色部分的面积不同,
∴指针落在两个区域的可能性不同.
∵用树状图求随机事件发生的概率时,应保证各种情况出现的可能性相同.
小亮的做法把左边转盘中的红色区域等分成2份,分别记作“红1”“红2”,保证了左边转盘中指针落在“蓝”“红1”“红2”三个区域的等可能性,因此是正确的.
(2)把C盘的红色区域等分成2份,分别记作“红1”“红2”,把D盘的蓝色区域等分成3份,分别记作“蓝1”“蓝2”“蓝3”,画树状图,如图所示.

一共有12种等可能的情况,其中可以“配成紫色”的情况有7种,
∴P(配成紫色)=$\frac{7}{12}$.
将非等可能事件转化为等可能事件的关键是把每个转盘都各自分为扇形的圆心角相等的几部分.
22.解:
(1)小颖的做法不正确,小亮的做法正确.
理由:
∵左边的转盘中红色部分和蓝色部分的面积不同,
∴指针落在两个区域的可能性不同.
∵用树状图求随机事件发生的概率时,应保证各种情况出现的可能性相同.
小亮的做法把左边转盘中的红色区域等分成2份,分别记作“红1”“红2”,保证了左边转盘中指针落在“蓝”“红1”“红2”三个区域的等可能性,因此是正确的.
(2)把C盘的红色区域等分成2份,分别记作“红1”“红2”,把D盘的蓝色区域等分成3份,分别记作“蓝1”“蓝2”“蓝3”,画树状图,如图所示.

一共有12种等可能的情况,其中可以“配成紫色”的情况有7种,
∴P(配成紫色)=$\frac{7}{12}$.
将非等可能事件转化为等可能事件的关键是把每个转盘都各自分为扇形的圆心角相等的几部分.
查看更多完整答案,请扫码查看


