《2025年新课程学习与检测九年级数学上册》

11. 一元二次方程 $ 3x(x - 2) = 7(x + 1) + 2 $ 的二次项系数、一次项系数及常数项之和为−19。

答案： 11.−19

12. 若关于 $ x $ 的一元二次方程 $ (m - 2)x^{2} + 2x + (m^{2} - 4) = 0 $ 有一个根是 $ 0 $,则 $ m = $−2。

答案： 12.−2

13. 如果关于 $ x $ 的方程 $ x^{2} - 3x + k = 0 $ 有两个相等的实数根,那么实数 $ k $ 的值是$\frac{9}{4}$。

答案： 13.$\frac{9}{4}$

14. 已知 $ a,b,c $ 是 $ \triangle ABC $ 的三边长,若方程 $ (a - c)x^{2} + 2bx + a + c = 0 $ 有两个相等的实数根,则 $ \triangle ABC $ 是直角三角形。

答案： 14.直角

15. 已知关于 $ x $ 的方程 $ x^{2} + (2k - 1)x + k^{2} - 1 = 0 $ 有两个实数根 $ x_{1},x_{2} $,若 $ x_{1},x_{2} $ 满足 $ x_{1}x_{2} + x_{1} + x_{2} = 3 $,则 $ k $ 的值为−1。

答案： 15.−1

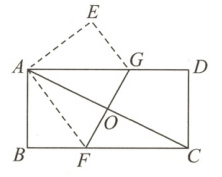
16. 如图所示,将一张矩形纸片 $ ABCD $ 折叠,使两个顶点 $ A,C $ 重合,折痕为 $ FG $. 若 $ AB = 4,BC = 8 $,则线段 $ BF $ 的长为3。

答案： 16.3

17. (6分)用适当的方法解下列方程:
(1) $ x^{2} - 6x + 1 = 0 $.
(2) $ x^{2} - 4 = 2x + 4 $.

答案： 1. （1）解：
对于一元二次方程$ax^{2}+bx + c = 0(a\neq0)$，其求根公式为$x=\frac{-b\pm\sqrt{b^{2}-4ac}}{2a}$。
在方程$x^{2}-6x + 1 = 0$中，$a = 1$，$b=-6$，$c = 1$。
先计算判别式$\Delta=b^{2}-4ac=(-6)^{2}-4×1×1=36 - 4=32$。
再代入求根公式：
$x=\frac{6\pm\sqrt{32}}{2}=\frac{6\pm4\sqrt{2}}{2}=3\pm2\sqrt{2}$。
所以$x_{1}=3 + 2\sqrt{2}$，$x_{2}=3 - 2\sqrt{2}$。
2. （2）解：
先将方程$x^{2}-4 = 2x + 4$化为一般形式：
$x^{2}-2x-8 = 0$。
对于一元二次方程$x^{2}-2x - 8 = 0$，其中$a = 1$，$b=-2$，$c=-8$。
分解因式得$(x - 4)(x+2)=0$（根据$x^{2}+(p + q)x+pq=(x + p)(x + q)$，这里$p=-4$，$q = 2$，$pq=-8$，$p + q=-2$）。
则$x-4 = 0$或$x + 2 = 0$。
解得$x_{1}=4$，$x_{2}=-2$。
综上，（1）$x_{1}=3 + 2\sqrt{2}$，$x_{2}=3 - 2\sqrt{2}$；（2）$x_{1}=4$，$x_{2}=-2$。

18. (5分)已知关于 $ x $ 的方程 $ 2x^{2} - (m + 2)x + 5 - m = 0 $ 的一个根为 $ 1 $,求它的另一个根及 $ m $ 的值.

答案： 18.解:根据题意得$2-(m + 2)+5 - m=0$，
　解得$m=\frac{5}{2}$。
　设另一个根为$x$，
　则$x·1=\frac{5 - m}{2}=\frac{5}{4}$，解得$x=\frac{5}{4}$，
∴另一个根为$\frac{5}{4}$。
∴它的另一个根为$\frac{5}{4}$，$m=\frac{5}{2}$。