《2025年新课程学习与检测九年级数学上册》

11. 将方程$(3 - 2x)(x + 2)=5$化为一般形式,为2x^{2}+x-1=0.

答案： $11.2x^{2}+x-1=0$

12. 已知代数式$x(x + 5)-6$与代数式$9x - 9$的值互为相反数,则$x=$1或-15.

答案： 12.1或-15

13. 若等腰三角形的底和腰是方程$(x - 3)(x - 6)=0$的两根,则这个等腰三角形的周长是15.

答案： 13.15

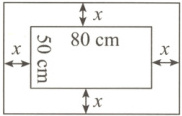
14. 如图所示,在一幅长80 cm、宽50 cm的矩形风景画的四周镶上一条金色纸边,制成一幅矩形挂图,如果要使整个挂图的面积是5 400 cm²,则金色纸边的宽为5cm.

答案： 14.5

15. 已知关于$x$的一元二次方程$x^{2}+2x - m^{2}-m = 0(m\gt0)$,当$m = 1,2,3,·s,2025$时,相应的一元二次方程的两个根分别记为$\alpha_{1},\beta_{1},\alpha_{2},\beta_{2},·s,\alpha_{2025},\beta_{2025}$,则$\frac{1}{\alpha_{1}}+\frac{1}{\beta_{1}}+\frac{1}{\alpha_{2}}+\frac{1}{\beta_{2}}+·s+\frac{1}{\alpha_{2025}}+\frac{1}{\beta_{2025}}$的值为\frac{4050}{2026}.

答案： $15.\frac{4050}{2026}$

16. (9分)解下列方程.
(1) $(x - 1)^{2}=9$.
(2) $3x^{2}=x$.
(3) $(x + 1)(x + 2)=2x + 4$.
(4) $x^{2}+4x + 3=0$.

答案： 1. （1）
解：
对于方程$(x - 1)^{2}=9$，根据平方根的定义$a^{2}=b(b\geq0)$，则$a=\pm\sqrt{b}$，这里$a = x - 1$，$b = 9$。
所以$x−1=\pm\sqrt{9}=\pm3$。
当$x - 1 = 3$时，$x=3 + 1=4$；
当$x - 1=-3$时，$x=-3 + 1=-2$。
所以$x_{1}=4$，$x_{2}=-2$。
2. （2）
解：
对于方程$3x^{2}=x$，移项得$3x^{2}-x = 0$。
提取公因式$x$，得$x(3x - 1)=0$。
根据$ab = 0$，则$a = 0$或$b = 0$，这里$a = x$，$b = 3x - 1$。
当$x = 0$时，方程成立；当$3x-1 = 0$时，$3x=1$，解得$x=\frac{1}{3}$。
所以$x_{1}=0$，$x_{2}=\frac{1}{3}$。
3. （3）
解：
对于方程$(x + 1)(x + 2)=2x + 4$，先将右边变形为$2(x + 2)$，则原方程变为$(x + 1)(x + 2)-2(x + 2)=0$。
提取公因式$(x + 2)$，得$(x + 2)[(x + 1)-2]=0$，即$(x + 2)(x - 1)=0$。
根据$ab = 0$，则$a = 0$或$b = 0$，这里$a=x + 2$，$b=x - 1$。
当$x + 2 = 0$时，解得$x=-2$；当$x - 1 = 0$时，解得$x = 1$。
所以$x_{1}=-2$，$x_{2}=1$。
4. （4）
解：
对于方程$x^{2}+4x + 3 = 0$，分解因式，根据$x^{2}+(a + b)x+ab=(x + a)(x + b)$，这里$a = 1$，$b = 3$，则$(x + 1)(x + 3)=0$。
根据$ab = 0$，则$a = 0$或$b = 0$，这里$a=x + 1$，$b=x + 3$。
当$x + 1 = 0$时，解得$x=-1$；当$x + 3 = 0$时，解得$x=-3$。
所以$x_{1}=-1$，$x_{2}=-3$。

17. (6分)关于$x$的一元二次方程$x^{2}-2ax - a + a^{2}=0$有实数根.
(1) 求$a$的取值范围.
(2) 若方程有两个不相等的实数根$x_{1},x_{2}$,且$x_{1}x_{2}=6$,求$a$的值.

答案： 17.解：
(1)由题意知，关于x的一元二次方程x^{2}-2ax-a+a^{2}=0有实数根，
$\therefore (-2a)^{2}-4 × 1 × (-a+a^{2}) \geqslant 0$，
解得$a \geqslant 0$，
$\therefore a$的取值范围是$a \geqslant 0$.
(2)$\because$方程有两个不相等的实数根$x_{1},x_{2}$，
$\therefore x_{1}x_{2}=-a+a^{2}$.
又$\because x_{1}x_{2}=6$，
$\therefore -a+a^{2}=6$，解得$a=-2$或$3$.
又$\because$当$a＞0$时方程有两个不相等的实数根，
$\therefore a=3$.