《2025年新课程学习与检测九年级数学上册》

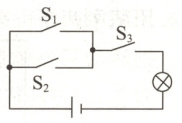
14. 某学校设置了以实践探究为主的个性化作业, 如图所示, 这是某学生设计的电路图, 随机闭合开关 $ S_1 $, $ S_2 $, $ S_3 $ 中的两个, 能使灯泡发光的概率是$\frac{2}{3}$.

答案： 14.$\frac{2}{3}$

15. 某中学在课后延时服务时段开发了戏曲、乐器、书法、棋类、球类五大兴趣课程. 现学校从这五类课程中随机抽取两类参加“全市青少年才艺展示活动”, 则恰好抽到“书画”和“乐器”的概率是$\frac{1}{10}$.

答案： 15.$\frac{1}{10}$

16. 在一个暗箱里放有 $ m $ 个除颜色外其他完全相同的小球, 这 $ m $ 个小球中红球只有 4 个, 每次将球搅匀后, 任意摸出 1 个球, 记下颜色再放回暗箱. 通过大量重复摸球试验后发现, 摸到红球的频率稳定在 25%, 那么可以推算 $ m $ 的值大约是16.

答案： 16.16

17. (8 分) 为提高学生的实践操作能力, 某市举行了理化实验操作考试, 有 A,B,C,D 四个实验可供选择, 规定每名学生只参加其中一个实验的考试, 并由学生自己抽签决定具体的考试实验, 欣欣、笑笑和佳佳都参加了本次考试.
(1) 欣欣参加实验 A 考试的概率为$\frac{1}{4}$.
(2) 请用列表法或画树状图的方法求出笑笑和佳佳抽到同一个实验的概率.

答案： 17.
(1)$\frac{1}{4}$
(2)解:列表，如下表所示.
笑笑 佳佳
A AA BA CA DA
B AB BB CB DB
C AC BC CC DC
D AD BD CD DD
所有等可能的情况有16种，其中笑笑和佳佳抽到同一个实验的情况有4种，
所以笑笑和佳佳抽到同一个实验的概率为$\frac{4}{16}$=$\frac{1}{4}$.

18. (8 分) 在一个不透明的口袋里装有红、黄两种颜色的乒乓球共 20 个(它们除颜色外都相同). 九年级(2)班的学习小组做摸球试验: 从袋中随机摸出 1 只球, 记下颜色后再把它放回原袋中搅匀, 进行重复试验, 并将试验数据统计如下(不完整, 其中频率值精确到 0.01).

(1) 填写表中空白处的数据. (结果精确到 0.01)
(2) 假如你去摸一次, 请估计你摸到黄球的概率, 你的估计值是0.20. (精确到 0.01)

答案： 18.
(1)0.81　0.80
(2)0.20　解析:由试验结果，结合频率和概率之间的关系可得，随机摸一次，摸到红球的概率为0.80，
因此,随机摸一次，摸到黄球的概率为1 - 0.80 = 0.20.

19. (8 分) 如图所示, 这是同一副扑克牌中的两张牌“黑桃 Q”和“黑桃 K”, 现在把这两张牌从中间剪断, 分成 4 张背面形状相同的半张牌, 并背面向上混合在一起搅匀. 嘉嘉和淇淇做游戏, 嘉嘉先从这 4 张半张牌中随机抽取 1 张(不放回), 淇淇接着再随机抽取 1 张.
(1) 嘉嘉抽到半张“黑桃 Q”的概率是$\frac{1}{2}$.

(2) 游戏规定: 所抽取的两张中, 能拼成一张完整的扑克牌, 则嘉嘉获胜; 否则, 淇淇获胜. 你认为这个游戏公平吗? 请用画树状图或列表的方法说明理由.

答案：
19.
(1)$\frac{1}{2}$　解析:4张背面形状相同的半张牌中，有两个“黑桃Q”和两个“黑桃K”，嘉嘉抽到每张的可能性相同，
∴嘉嘉抽到半张“黑桃Q”的概率是$\frac{2}{4}$=$\frac{1}{2}$.
(2)解:用列表法表示所有可能出现的结果，如下表所示.

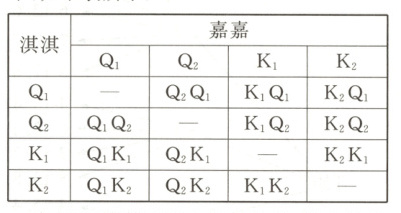
一共有12种等可能出现的结果，其中能拼成一张完整的扑克牌的结果有4种，
∴能拼成一张完整的扑克牌的概率是$\frac{4}{12}$=$\frac{1}{3}$，不能拼成一张完整的扑克牌的概率是$\frac{2}{3}$.
∴他们获胜的概率不相等，游戏不公平.