《2025年新课程学习与检测九年级数学上册》

15. (8分)反比例函数$y = \frac{k}{x}$的图象经过点$A(-2,3)$.
(1)求这个函数的表达式.
(2)请判断点$B(1,6)$是否在这个反比例函数的图象上,并说明理由.

答案： 15.解：
(1)
∵反比例函数$y = \frac{k}{x}$的图象经过点A(-2,3)，
∴k = xy = (-2) × 3 = -6.
∴该函数的表达式为$y = - \frac{6}{x}.$
(2)点B(1,6)不在这个反比例函数的图象上.
理由：由
(1)知k = -6.
∵1 × 6 = 6 ≠ -6，
∴点B(1,6)不在这个反比例函数的图象上.

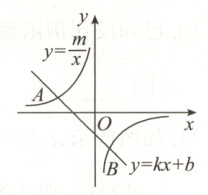
16. (8分)如图所示,已知$A(-4,2)$,$B(n,-4)$是一次函数$y = kx + b$的图象与反比例函数$y = \frac{m}{x}$的图象的两个交点.
(1)求此反比例函数和一次函数的表达式.
(2)根据图象写出使一次函数的值小于反比例函数的值的$x$的取值范围.

答案： 16.解：
(1)把点A(-4,2)的坐标代入$y = \frac{m}{x}，$
得m = -4 × 2 = -8，
∴反比例函数的表达式为$y = - \frac{8}{x}.$
把点B(n,-4)的坐标代入$y = - \frac{8}{x}，$
得-4n = -8，解得n = 2，
∴点B的坐标为(2,-4).
把点A(-4,2),B(2,-4)的坐标分别代入y = kx + b，
得$\begin{cases}-4k + b = 2, \\ 2k + b = -4,\end{cases}$解得$\begin{cases}k = -1, \\ b = -2,\end{cases}$
∴一次函数的表达式为y = -x - 2.
(2)由图象可知，x的取值范围是 -4 ＜ x ＜ 0或x ＞ 2.

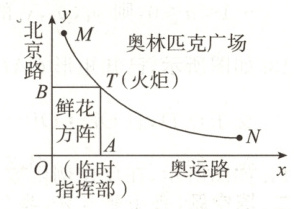
17. (8分)如图所示,奥运火炬抵达某市奥林匹克广场后,沿图中直角坐标系中的一段反比例函数图象传递.动点$T(s,t)$表示火炬的位置,火炬从离北京路$10\ m$处的$M$点开始传递,到离北京路$1000\ m$的$N$点时传递活动结束.临时指挥部设在坐标原点$O$(北京路与奥运路的十字路口),$OATB$为鲜花方阵,方阵始终保持矩形形状且面积恒为$10000\ m^2$(路线宽度均不计).
(1)求图中反比例函数的关系式.(不需写出自变量的取值范围)
(2)当鲜花方阵的周长为$500\ m$时,确定此时火炬的位置.(用坐标表示)

答案： 17.解：
(1)设反比例函数为$y = \frac{k}{x}(k ＞ 0)，$
则$k = xy = st = S_{矩形OATB} = 10000，$
∴$y = \frac{10000}{x}.$
(2)设鲜花方阵的长为sm，则宽为(250 - s)m，
由题意得s(250 - s) = 10000，
即$250s - s^2 = 10000，$
即$s^2 - 250s + 10000 = 0，$
解得s = 50或s = 200，均满足题意.
∴此时火炬的坐标为(50,200)或(200,50).