《2025年新课程学习与检测九年级数学上册》

17. (6分)如图所示,已知点D,E分别在边AB,AC上,BE,CD相交于点O,$\frac{AD}{AB}=\frac{DE}{BC}=\frac{DO}{CO}$,$AB=7$,$DB=4$,$BC=9$,$CD=10$,求DE,CO的长.

答案： 17.DE的长为$\frac{27}{7}$,CO的长为7.

18. (6分)如图所示,在$Rt\triangle ABC$中,$\angle C=90^{\circ}$,$AC=6$ cm,$BC=8$ cm,设P,Q分别为AC,AB上的动点,在点P自点A沿AC方向以1 cm/s的速度向点C匀速移动的同时,点Q自点B沿BA方向以2 cm/s的速度向点A匀速移动,当Q点到达A点时,P点就停止移动.设P,Q移动的时间为t s.
(1)当t为何值时,$AP=PQ$?
(2)$\triangle APQ$能否与$Rt\triangle ABC$相似?若能,求出t的值;若不能,请说明理由.

答案： 18.
(1)$\frac{25}{8}$.
(2)能.当t=$\frac{30}{11}$或$\frac{50}{13}$时,△APQ与Rt△ABC相似.

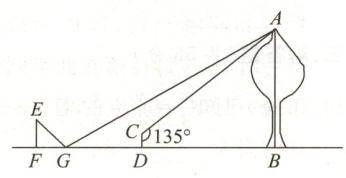
19. (6分)小明利用刚学过的测量知识来测量学校内一棵古树的高度.一天下午,他和学习小组的同学带着测量工具来到这棵古树前,由于有围栏保护,他们无法到达古树的底部B,如图所示.于是,他们先在古树周围的空地上选择一点D,并在点D处安装了测量器CD,测得$\angle ACD=135^{\circ}$;再在BD的延长线上确定一点G,使$DG=5$ m,并在G处的地面上水平放置了一个小平面镜.小明沿着BG方向移动,当移动到点F时,他刚好在小平面镜内看到这棵古树的顶端A的像,此时,测得$FG=2$ m,小明的眼睛与地面的距离$EF=1.6$ m,测量器的高度$CD=0.5$ m.已知点F,G,D,B在同一水平直线上,且EF,CD,AB均垂直于FB,则这棵古树的高度AB为多少?(小平面镜的大小忽略不计)

答案： 19.18m.

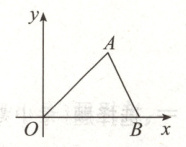
20. (6分)如图所示,在平面直角坐标系中,已知$\triangle OAB$,点A的坐标为$(a,a)$,点B的坐标为$(b,0)$.若a,b的值是关于x的一元二次方程$x^{2}-5x+6=0$的两个根,且$b＞a$.
(1)$a=$2,$b=$3.
(2)若点P在y轴上,且$\triangle POA\backsim\triangle AOB$,求点P的坐标.

答案： 20.
(1)2　3　
(2)(0,$\frac{8}{3}$).