《2026年万唯中考试题研究数学河北专版》

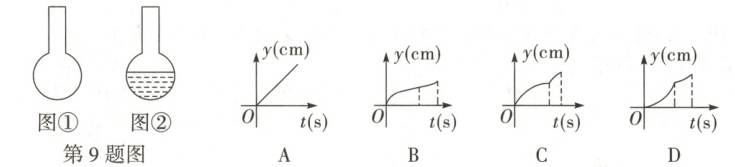
9. 万唯原创 如图①是一个圆底烧瓶,李老师在做化学实验时向空瓶内匀速加水至图②状态停止,记加水时长为 $ t(s) $,圆底烧瓶里水面的高度为 $ y(cm) $,则 y 与 t 关系的图象大致是(B)

答案： 9. B

10. 万唯原创 如图,在菱形 ABCD 中, $ ∠A = 120^{\circ} $,DM 平分 $ ∠ADB $交 AB 于点 M,过点 M 作 $ MN⊥AB $交 BD 于点 N,则 $ \frac{CD}{DN} $的值为(C)

A.2
B.$ \sqrt{2} $
C.1
D.$ \sqrt{3} - 1 $

答案： 10. C

11. 万唯原创 如图,正六边形 ABCDEF 和正六边形 GHIJKL 均以点 O 为中心,连接 AG,BH,CI,DJ,EK, FL(A,G,H 三点共线),若 $ CI = 2 $, $ IJ = 3 $,则正六边形 ABCDEF 的边长为(C)

A.$ \sqrt{3} $
B.5
C.$ \sqrt{19} $
D.19

答案： 11. C

12. 在平面直角坐标系中,点 A 的坐标为 $ (0,3) $,点 B 的坐标为 $ (-2,2) $.将二次函数 $ y = mx^{2} - 2mx + m - 2(m ≠ 0) $的图象先向左平移 $ a(a＞0) $个单位长度,再向上平移 $ b(b＞0) $个单位长度得到图象 M,使得图象 M 的顶点落在线段 AB 上.关于 a,b 的取值,三人的说法如下:甲: $ a = 1 $, $ b = 5 $;乙: $ a = 2 $, $ b = \frac{9}{2} $;丙: $ a = 3 $, $ b = 4 $.
下列判断正确的是(D)

A.只有甲和乙对
B.只有甲和丙对
C.只有乙和丙对
D.甲、乙、丙都对

答案： 12. D

13. 新考法 结论开放 (2025 定心卷)若 $ \underbrace{(-2)×(-2)×…×(-2)}_{n个-2相乘(n＞3)} ＜ 0 $,则 n 的值可以为5(答案不唯一)(写出一个即可).

答案： 13. 5(答案不唯一)

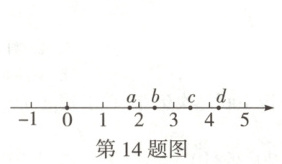
14. 如图,a,b,c,d 是数轴上的点,则 $ \sqrt{3}×\sqrt{2} $在数轴上对应的点可能是b.

答案： 14. b

15. 万唯原创 已知在平面直角坐标系中,反比例函数 $ y = \frac{k}{x}(x ＜ 0) $的图象如图所示,点 $ A(-4,4) $,连接 OA,过点 A 作 y 轴的垂线,垂足为点 B.当反比例函数 $ y = \frac{k}{x}(x ＜ 0) $的图象把线段 OA 上横、纵坐标均为整数的点分布在其左右两侧,且左侧点的个数:右侧点的个数 $ = 3:2 $时,k 的取值范围为-4＜k＜-1.

答案： 15. -4＜k＜-1

16. 如图,点 D 是 $ Rt△ABC $斜边 AB 的中点,连接 CD,将 $ △CBD $沿 CD 翻折,点 B 落在点 E 处,连接 BE,交 CD 于点 M,交 CA 于点 N,连接 AE.若点 N 是 EM 的中点,则 $ sin∠ACE = $\frac{1}{3}.

答案： $16. \frac{1}{3}$