第4页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
8. (2025黑白卷)某校就“每周在校体育锻炼时间”的问题抽取了一部分中学生调查,并将调查结果绘制成如图的统计图. 其中分组:$ A $组:$ 5 \leqslant h < 6 $;$ B $组:$ 6 \leqslant h < 7 $;$ C $组:$ 7 \leqslant h < 8 $;$ D $组:$ 8 \leqslant h < 9 $;$ E $组:$ 9 \leqslant h \leqslant 10 $($ h $为每周在校锻炼时间,单位:小时). 若第二周$ A $组学生的锻炼时间均不小于6小时,其他学生的锻炼时间不变,且使新的结果的中位数一定与原来的中位数所在组相同,则第二周$ D $组的学生数最多为 (
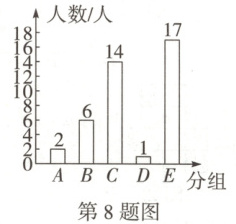
A.1
B.2
C.3
D.无法确定
B
)
A.1
B.2
C.3
D.无法确定
答案:
8.B
9. 万唯原创 如图,将$ □ ABCD $折叠,使得折叠后点$ A $落在$ BC $边上的点$ A' $处,点$ B $落在点$ B' $处,$ EF $是折痕,若$ \angle BFE=115^{\circ},\angle FA'B'=20^{\circ} $,则$ \angle C $的度数为 (
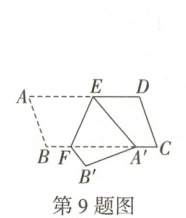
A.$ 50^{\circ} $
B.$ 65^{\circ} $
C.$ 70^{\circ} $
D.$ 75^{\circ} $
C
)
A.$ 50^{\circ} $
B.$ 65^{\circ} $
C.$ 70^{\circ} $
D.$ 75^{\circ} $
答案:
9.C
10. 万唯原创 在$ (\sqrt{27}-\sqrt{\frac{1}{3}})× □ $中的“$ □ $”内填入实数,使其结果为有理数. 对于嘉嘉、淇淇的说法判断正确的是 (
嘉嘉说:“可以填入$ \sqrt{3} $.”
淇淇说:“可以填入$ \sqrt{\frac{1}{3}} $.”
A.嘉嘉的说法对,淇淇的说法不对
B.嘉嘉的说法不对,淇淇的说法对
C.嘉嘉和淇淇的说法都对
D.嘉嘉和淇淇的说法都不对
C
)嘉嘉说:“可以填入$ \sqrt{3} $.”
淇淇说:“可以填入$ \sqrt{\frac{1}{3}} $.”
A.嘉嘉的说法对,淇淇的说法不对
B.嘉嘉的说法不对,淇淇的说法对
C.嘉嘉和淇淇的说法都对
D.嘉嘉和淇淇的说法都不对
答案:
10.C
11. 如图,在正六边形$ ABCDEF $中,作正五边形$ HKCDG $,连接$ BK $,则$ \angle ABK $的度数为 (
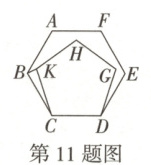
A.$ 45^{\circ} $
B.$ 36^{\circ} $
C.$ 30^{\circ} $
D.$ 27^{\circ} $
B
)
A.$ 45^{\circ} $
B.$ 36^{\circ} $
C.$ 30^{\circ} $
D.$ 27^{\circ} $
答案:
11.B
12. 万唯原创 已知抛物线$ y_{1}=-(x-m)^{2},y_{2}=-(x-n)^{2},n-m=2 $,直线$ x=2 $与抛物线$ y_{1},y_{2} $分别交于点$ A(2,p),B(2,q) $,当$ p < q $时,$ n $的值可以是 (
A.6
B.5
C.3
D.0
D
)A.6
B.5
C.3
D.0
答案:
12.D
13. 定义新运算:对于任意实数$ a,b $均有$ a※b=a(a-b)+1 $,则不等式$ 4※x \geqslant 1 $的解集为
x\leq4
.
答案:
$13.x\leq4$
14. 万唯原创 如图,正方形$ ABCD $的顶点$ A,B $分别与数轴上表示数$ 0,2 $的点重合. 点$ C $在$ \odot A $上,则$ \odot A $与数轴正半轴的交点$ E $表示的数为
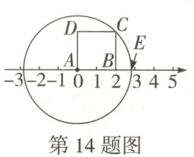
2\sqrt{2}
.
答案:
$14.2\sqrt{2}$
15. 如图,线段$ AB $与$ y $轴平行,点$ A $的坐标为$ (-1,a) $,将线段$ AB $沿着$ x $轴水平向左平移得到线段$ CD $,点$ B $的对应点$ D $的坐标为$ (-3,a+6) $,若反比例函数$ y=\frac{k}{x}(x < 0) $的图象同时经过点$ B $和点$ C $,则$ k $的值为
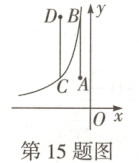
-9
.
答案:
15.-9
16. 万唯原创 如图,$ \triangle ABC $是等腰直角三角形,$ AC=BC=3 $,点$ D,E $分别在$ AC,BC $边上,且$ CD=CE=\sqrt{2} $,连接$ DE $,将$ \triangle CDE $绕点$ C $逆时针旋转$ \alpha (0^{\circ} \leqslant \alpha \leqslant 90^{\circ}) $,连接$ AD $,当$ DE // CB $时,点$ E $到直线$ AD $的距离为
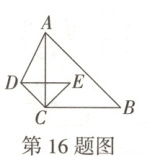
\frac{4\sqrt{5}}{5}
.
答案:
$16.\frac{4\sqrt{5}}{5}$
查看更多完整答案,请扫码查看


