《2026年万唯中考试题研究数学河北专版》

4. (8分)在平面直角坐标系中,函数$y = kx + b(k \neq 0)$的图象由$y = 3x$的图象平移得到,且与平行于x轴的直线交于点$(\frac{b}{2},5)$.
(1)求$k,b$的值;
(2)当$x ＞ 1$时,对于x的每一个值,函数$y = mx + k$的值小于函数$y = kx + b(k \neq 0)$的值且大于5,求$m$的值.

答案： 4.
(1)k = 3,b = 2;
(2)m = 2.

5. (8分)万唯原创 如图,在$\odot O$中,线段AB与$\odot O$相切于点A,点C在线段AB上,且$BC = 6$,$CD,BE$分别与$\odot O$相切于点D,E,$\angle ACD = 60^{\circ}$.
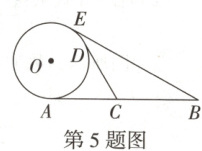
(1)设$\odot O$的半径为$r$,用含$r$的代数式表示A,D之间的距离;
(2)连接$OB$,若$\sin \angle OBE = \frac{1}{4}$,求$\odot O$的直径.

答案：
5.解:
(1)如解图①,连接OA,OC,OD,AD,记AD与OC交于点F,
∴OF⊥AD,AD = 2AF.
∵CD与⊙O相切于点D,CA与⊙O相切于点A,
∴∠OAC = ∠ODC = 90°.
∵OC = OC,OA = OD,
∴Rt△OAC≌Rt△ODC(HL),
∴∠DCO = ∠ACO = $\frac{1}{2}$∠ACD = 30°,∠AOF = 60°,
∴在Rt△AOF中,AF = OA·sin60° = $\frac{\sqrt{3}}{2}$r,
∴AD = 2AF = $\sqrt{3}$r,
∴A,D之间的距离为$\sqrt{3}$r;


(2)如解图②,连接OA,OE.
∵BE与⊙O相切于点E,BA与⊙O相切于点A,
∴∠OAB = ∠OEB = 90°.
∵OB = OB,OA = OE,
∴Rt△OAB≌Rt△OEB(HL),
∴∠EBO = ∠ABO.
∵sin∠OBE = $\frac{1}{4}$,
∴sin∠ABO = $\frac{1}{4}$,
∴在Rt△OAB中,tan∠ABO = $\frac{\sqrt{15}}{15} = \frac{AO}{AB}$,
∴AB = $\sqrt{15}$OA.
∵BC = 6,AB - AC = BC,
由
(1)得AC = $\sqrt{3}$OA,
∴$\sqrt{15}$OA - $\sqrt{3}$OA = 6,
解得OA = $\frac{\sqrt{15} + \sqrt{3}}{2}$,
∴⊙O的直径为$\sqrt{15} + \sqrt{3}$