《2026年万唯中考试题研究数学河北专版》

17. （8分）如图，在矩形ABCD中，AC是对角线.
（1）过点B作AC的垂线，与AC交于点E（要求：尺规作图，保留作图痕迹，不写作法）；
（2）在（1）的条件下，若$AD = 3$，$CD = 4$，求$\triangle ABE$的周长.

答案：
17.解:
(1)如解图,点E即为所求;
(2)△ABE的周长为$\frac{48}{5}$.

18. （8分）（2025黑白卷）食用果蔬前，适当浸泡可降低农药的残留. 某检测小组针对同种瓜果蔬菜研究了采用清水浸泡不同时长对某种农药去除率的影响. 记浸泡时间为t分钟，农药的去除率为y%，部分实验数据记录如图.
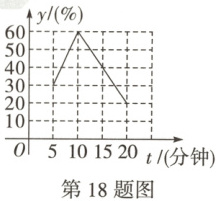
（1）通过分析实验数

据

，发现可以用两个一次函数刻画农药的去除率y（%）与浸泡时间t（分钟）之间的关系，试求y与t之间的函数解析式；
（2）检测小组成员嘉嘉将一部分瓜果蔬菜用清水浸泡8分钟，淇淇将同种类型和数量的瓜果蔬菜用清水浸泡12分钟，猜想哪位成员检测出的农药的去除率更高？并说明理由.

答案： 1. （1）
当$5\lt t\leqslant10$时：
设$y = k_1t + b_1$（$k_1\neq0$），把$(5,30)$，$(10,60)$代入$y = k_1t + b_1$得：
$\begin{cases}5k_1 + b_1 = 30\\10k_1 + b_1 = 60\end{cases}$
用第二个方程减去第一个方程：$(10k_1 + b_1)-(5k_1 + b_1)=60 - 30$。
即$10k_1 + b_1 - 5k_1 - b_1 = 30$，$5k_1=30$，解得$k_1 = 6$。
把$k_1 = 6$代入$5k_1 + b_1 = 30$，得$5×6 + b_1 = 30$，$b_1 = 0$。
所以$y = 6t(5\lt t\leqslant10)$。
当$10\lt t\leqslant20$时：
设$y = k_2t + b_2$（$k_2\neq0$），把$(10,60)$，$(20,20)$代入$y = k_2t + b_2$得：
$\begin{cases}10k_2 + b_2 = 60\\20k_2 + b_2 = 20\end{cases}$
用第二个方程减去第一个方程：$(20k_2 + b_2)-(10k_2 + b_2)=20 - 60$。
即$20k_2 + b_2 - 10k_2 - b_2=-40$，$10k_2=-40$，解得$k_2=-4$。
把$k_2=-4$代入$10k_2 + b_2 = 60$，得$10×(-4)+b_2 = 60$，$b_2 = 100$。
所以$y=-4t + 100(10\lt t\leqslant20)$。
综上，$y=\begin{cases}6t(5\lt t\leqslant10)\\-4t + 100(10\lt t\leqslant20)\end{cases}$。
2. （2）
嘉嘉：当$t = 8$（$5\lt8\leqslant10$）时，代入$y = 6t$，得$y_1=6×8 = 48$。
淇淇：当$t = 12$（$10\lt12\leqslant20$）时，代入$y=-4t + 100$，得$y_2=-4×12 + 100=-48 + 100 = 52$。
因为$y_1 = 48$，$y_2 = 52$，$48\lt52$。
所以淇淇检测出的农药的去除率更高。