《2026年万唯中考试题研究数学河北专版》

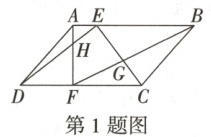
1. 万唯原创 如图,E,F 分别是$□ ABCD$的边 AB,CD 上的点,AF 与 DE 相交于点 H,BF 与 CE 相交于点 G,若$S_{△AHD}=a,S_{△BGC}=b$,则四边形 HEGF 的面积为 (A)

A.$ a + b $
B.$ b - a $
C.$ 2a - b $
D.$ 2a + b $

答案： 1. A

2. 将 1,2,3,4,5,···,37 这 37 个连续整数不重不漏地填入 37 个空格中. 要求:从左至右,第 1 个数是第 2 个数的倍数,第 1 个数与第 2 个数之和是第 3 个数的倍数,第 1,2,3 个数之和是第 4 个数的倍数,···,前 36 个数的和是第 37 个数的倍数. 若第 1 个空格填入 37,第 37 个空格所填入的数为 (B)


A.5
B.19
C.21
D.32

答案： 2. B

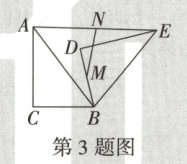
3. 万唯原创 如图,在$ \triangle ABC $中,$ \angle C = 90^{\circ},AC = 4,BC = 3 $,将$ \triangle ABC $绕点 B 顺时针旋转,得到$ \triangle EBD $,连接 AE. 若 M,N 分别为 BD,AE 的中点,则线段 MN 长的最小值为 \frac{1}{2} .

答案： 3. $\frac{1}{2}$

4. (2025 黑白卷)

如

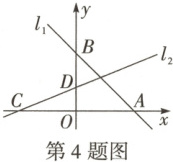
图,在平面直角坐标系中,直线 $ l_1 $ 分别交 x 轴、y 轴正半轴于点 $ A(4,0) $,B,点 C 在 x 轴负半轴,且 $ OC = OA = OB $,直线 $ l_2 $ 过点 C,交 y 轴于点 $ D(0,b) $.
(1)求直线 $ l_1 $ 的解析式;
(2)若 $ b = 2 $,求点 D 到直线 $ l_1 $ 的距离;
(3)若直线 $ l_2 $ 与线段 AB 交于点 E(不与点 A,B 重合).
①当$ \triangle OCD $与$ \triangle BDE $的面积相等时,求点 E 的坐标;
②当点 E 的横坐标不大于纵坐标时,直接写出点 b 的取值范围.

答案：
4. 解：
(1)
∵$A(4,0)$，$OA = OB$，
∴点$B(0,4)$。
设直线$l_1$的解析式为$y = kx + n$，将点$A(4,0)$，$B(0,4)$的坐标分别代入$y = kx + n$中，
得$\begin{cases}0 = 4k + n\\4 = n\end{cases}$，
解得$\begin{cases}k = -1\\n = 4\end{cases}$，
∴直线$l_1$的解析式为$y = -x + 4$；
(2)如解图，过点$D$作$DH⊥AB$于点$H$。

∵$OA = OB = 4$，$\angle AOB = 90^{\circ}$，
∴$\angle ABO = 45^{\circ}$，
∴$\triangle BHD$是等腰直角三角形。
∵$b = 2$，
∴$OD = 2$，
∴$BD = OB - OD = 2$，
∴$BH = DH = \frac{\sqrt{2}}{2}BD = \sqrt{2}$，
∴点$D$到直线$l_1$的距离为$\sqrt{2}$；
(3)①设$E(m,-m + 4)$。
∵$S_{\triangle OCD} = S_{\triangle BDE}$，
∴$S_{\triangle ECA} = S_{\triangle BOA}$，
即$\frac{1}{2}AC· y_E = \frac{1}{2}OA· OB$，
∴$\frac{1}{2}×8×(-m + 4) = \frac{1}{2}×4×4$，
解得$m = 2$，
∴$-m + 4 = 2$，
∴点$E$的坐标为$(2,2)$；
②$\frac{4}{3} \leq b ＜ 4$。
[解法提示]
∵直线$l_2$过点$C(-4,0)$，$D(0,b)$，
∴直线$l_2$的解析式为$y = \frac{b}{4}x + b$，当直线$l_2$过点$A(4,0)$时，$\frac{b}{4}×4 + b = 0$，
∴$b = 0$，当直线$l_2$过点$B(0,4)$时，$b = 4$，
∴当$0 ＜ b ＜ 4$时，直线$l_2$与线段$AB$有交点，联立$\begin{cases}y = -x + 4\\y = \frac{b}{4}x + b\end{cases}$，
解得$\begin{cases}x = \frac{16 - 4b}{4 + b}\\y = \frac{8b}{4 + b}\end{cases}$，
∴直线$l_2$与线段$AB$的交点$E(\frac{16 - 4b}{4 + b},\frac{8b}{4 + b})$。
∵交点$E$的横坐标不大于纵坐标，
∴$\frac{16 - 4b}{4 + b} \leq \frac{8b}{4 + b}$，即$16 - 4b \leq 8b$，解得$b \geq \frac{4}{3}$。
综上所述，$\frac{4}{3} \leq b ＜ 4$。