第54页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
9. (2025 黑白卷)在数论领域中,有时需要略去一个实数的小数部分只研究它的整数部分,或需要略去整数部分只研究小数部分,因而引入高斯记号。若 $ x $ 为任意数,取不大于 $ x $ 的最大整数记为 $ [x] $,取 $ x $ 与 $ [x] $ 的差记为 $ \{ x \} $。例:$ \{ -\frac{5}{4} \} = (-\frac{5}{4}) - [-\frac{5}{4}] = -\frac{5}{4} - (-2) = \frac{3}{4} $。若 $ 4 < a < 5 $,则 $ \{ a \} - \{ -2.7 \} $ 的值可以为(
A.$ -2 $
B.$ -1.5 $
C.$ 0.5 $
D.1
C
)A.$ -2 $
B.$ -1.5 $
C.$ 0.5 $
D.1
答案:
9.C
10. 万唯原创 如图,在平面直角坐标系中,$ A(-2,2) $,$ B(6,2) $,$ C(2,3) $,点 $ D $ 是线段 $ AB $ 上一点(不与点 $ A $,$ B $ 重合),直线 $ CD $ 的解析式为 $ y = kx + b(k \neq 0) $,当 $ y $ 随 $ x $ 的增大而减小时,点 $ D $ 的坐标可以是(
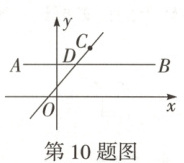
A.$ (-2,2) $
B.$ (2,2) $
C.$ (3,2) $
D.$ (7,2) $
C
)
A.$ (-2,2) $
B.$ (2,2) $
C.$ (3,2) $
D.$ (7,2) $
答案:
10.C
11. 为了解初三学生的视力情况,将初三年级的 500 名同学从 1 到 500 编号,并按编号从小到大的顺序站成一排报数 1、2、3、…,报到非 3 的倍数的退下,3 的倍数的留下,留下的同学从编号小的开始继续报数 1、2、3、…,报到非 3 的倍数的退下,3 的倍数的留下,…,如此继续,直到最后留下两名同学,则最后留下的两名同学编号是(
A.3,9
B.252,486
C.243,486
D.243,498
C
)A.3,9
B.252,486
C.243,486
D.243,498
答案:
11.C
12. 万唯原创 在矩形 $ ABCD $ 中,$ AB = 6 $,$ BC = 8 $,要求在矩形 $ ABCD $ 内部画出一个三角形,使得其一边上的中线等于这条边的一半。甲、乙、丙分别画出了如图所示的三角形(阴影部分),则符合作图要求的是(
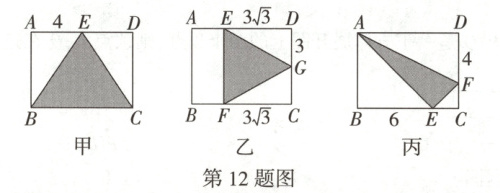
A.只有甲
B.只有乙
C.只有丙
D.乙,丙
C
)
A.只有甲
B.只有乙
C.只有丙
D.乙,丙
答案:
12.C
13. 若 $ (\sqrt{7} ÷ \sqrt{14}) × \sqrt{\frac{a}{b}} = 1 $,则 $ \frac{a}{b} = $
2
。
答案:
13.2
14. 某课题研究小组成员由一名组长和四名组员(两男两女)组成。某次研讨会上,组长选择座位 $ E $ 就座,四名成员随机选择剩余座位落座,座位分布如图所示,则两名女组员座位相邻的概率为
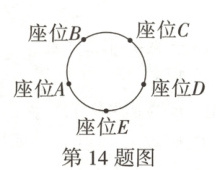
$\frac{1}{2}$
。
答案:
14.$\frac{1}{2}$
15. 如图,$ G $ 是正六边形 $ ABCDEF $ 对角线 $ BF $ 上一点,且 $ BG = 3FG $,连接 $ FC $,$ EG $,若 $ \triangle EFG $ 的面积为 1,则 $ \triangle FBC $ 的面积为
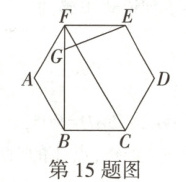
4
。
答案:
15.4
16. 万唯原创 双曲线 $ L: y = \frac{6}{x}(x > 0) $ 如图所示,小李设计了一个程序:对于数对 $ (a,b) $ 表示输入两个正数 $ a $,$ b $,可得双曲线 $ L': y = \frac{ab}{x}(x > 0) $,直线 $ l: y = 2 $ 分别与双曲线 $ L $,$ L' $ 交于点 $ A $,$ B $(点 $ B $ 与点 $ A $ 不重合),连接 $ OA $,$ OB $,若 $ S_{\triangle AOB} < 2.5 $,则线段 $ AB $ 上横坐标为正整数的点(不含端点)最多有
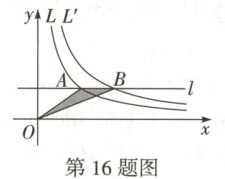
2
个。
答案:
16.2
查看更多完整答案,请扫码查看


