《2026年万唯中考试题研究数学河北专版》

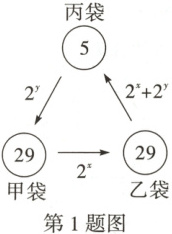
1. 如图，在甲、乙、丙三只袋中分别装有球29个、29个、5个，先从甲袋中取出$2^{x}$个球放入乙袋，再从乙袋中取出$(2^{x}+2^{y})$个球放入丙袋，最后从丙袋中取出$2^{y}$个球放入甲袋，此时三只袋中球的个数都相同，则$2^{x+y}$的值等于(A)

A.128
B.64
C.32
D.16

答案： A

2. 如图，在平面直角坐标系中，$\triangle ABC$的顶点A，B的坐标分别为$(-2,2)$，$(-4,-4)$，$BC// x$轴，以AB，BC为边作平行四边形ABCD，点D恰好在y轴上，将$\triangle ABC$沿CD向上平移得到$\triangle A_{1}B_{1}C_{1}$，当边BC扫过图形的面积为6时，点$A_{1}$的坐标为(D)

A.$(-2,6)$
B.$(-2,5)$
C.$(-1,6)$
D.$(-1,5)$

答案： D

3. 如图，在正方形ABCD中，P，Q分别是AD，BC上的点(不与点D，C重合)，$PQ// AB$，BD与PQ交于点E，取DE的中点F，连接AQ，FQ，则$\frac {AQ}{QF}$的值为$\sqrt{2}$.

答案： $\sqrt{2}$

4. 如图，扇形AOB和扇形COD的圆心角均为$120^{\circ }$，其中扇形AOB保持不动，扇形COD绕点O旋转，已知$AO=6$，$CO=3\sqrt {2}$.
（1）如图①，连接AC.
①若AC与$\widehat {CD}$所在圆相切，求$∠AOC$的度数；
②当$\triangle AOC$的面积最大时，求AC的长；
（2）如图②，连接AB，当点C落在线段AB上时，直接写出扇形AOB与扇形COD重合部分的面积.

答案：
解:
(1)①
∵AC与$\odot O$CD所在圆相切，
∴OC⊥AC，即∠ACO=90°，
∴$\cos\angle AOC=\frac{OC}{AO}=\frac{3\sqrt{2}}{6}=\frac{\sqrt{2}}{2}$，
∴∠AOC=45°；
②
∵AO的长为定值，
∴当△AOC的面积最大时，即OC⊥AO.
在Rt△AOC中，由勾股定理可得
$AC=\sqrt{AO^{2}+OC^{2}}=3\sqrt{6}$；
(2)$\frac{3}{4}\pi$或$\frac{21}{4}\pi$.
[解法提示]情形一:如解图①,过点O作OE⊥AB于点E.
∵OA=OB，∠AOB=120°，
∴∠BAO=30°，∠AOE=∠BOE=$\frac{1}{2}$∠AOB=60°，
∴$OE=\frac{1}{2}AO=3$，
∴$\cos\angle EOC=\frac{OE}{OC}=\frac{\sqrt{2}}{2}$，
∴∠EOC=45°，
∴∠COB=60° - ∠EOC=15°，
∴重合部分的面积为$\frac{15}{360}×(3\sqrt{2})^{2}×\pi=\frac{3}{4}\pi$；情形二:如解图②,过点O作OF⊥AB于点F,同理可得$OF=\frac{1}{2}AO=3$，∠AOF=∠BOF=60°，
∴$\cos\angle FOC=\frac{OF}{OC}=\frac{\sqrt{2}}{2}$，
∴∠FOC=45°，
∴∠COB=∠COF+∠BOF=105°，
∴重合部分的面积为$\frac{105}{360}×(3\sqrt{2})^{2}\pi=\frac{21}{4}\pi$.
综上所述，扇形AOB与扇形COD重合部分的面积为$\frac{3}{4}\pi$或$\frac{21}{4}\pi$.