《2026年万唯中考试题研究数学河北专版》

1. (8分)(1)简便运算：$-\frac{2}{3}× 5+(-1\frac{1}{3})× 5-1× (-5)$；
(2)化简：$\frac{x^{2}-4x + 4}{x + 2}÷ (1 - \frac{4}{x + 2})$。

答案：
(1)原式=-5；
(2)原式=x-2.

2. (8分)如图，在$\triangle ABC$中，过点$C$作$AB$的垂线交$AB$于点$D$，$E$为$CD$上一点，连接$AE$，$BE$，若$AD = DE$，$BD = CD$。
(1)求证：$\triangle ACD\cong\triangle EBD$；
(2)若$AE = CE$，求$\angle BEC$的度数。

答案：
(1)证明略；
(2)∠BEC的度数为112.5°.

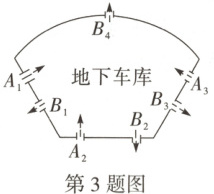
3. (8分)如图是某商业中心地下停车场的平面图，共有$A_{1}$，$A_{2}$，$A_{3}$三个入口，$B_{1}$，$B_{2}$，$B_{3}$，$B_{4}$四个出口，假设顾客选择各个出入口的机会均等。
(1)某顾客从$A_{3}$入口进入地下车库的概率为$\frac{1}{3}$；
(2)请用列表或画树状图的方法，求某顾客进出地下车库出入口数字序号相同的概率。

答案：
(1)$\frac{1}{3}$；
(2)列表或画树状图略，某顾客进出地下车库出入口数字序号相同的概率为$\frac{1}{4}$.