《2026年万唯中考试题研究数学河北专版》

10. “科学用眼，保护视力”是青少年珍爱生命的具体表现. 科学证实：近视眼镜的度数y(度)与镜片焦距x(m)成反比例关系. 500度近视眼镜片的焦距为0.2m，y与x函数关系的图象大致如图，则下列说法不正确的是(D)

A.y与x的函数解析式是$y = \frac{100}{x}(x ＞ 0)$
B.当$x = 0.25$时，$y = 400$
C.随着焦距的减小，眼镜度数逐渐增大
D.当$0.1 ＜ x ＜ 0.5$时，$y ＜ 1000$

答案： 10.D

11. 若关于x的一元二次方程$x^{2} - 3x + t = 0$有两个不相等的实数根，则t的值不可以是(C)

A.0
B.$-1$
C.3
D.$\sqrt{3}$

答案： 11.C

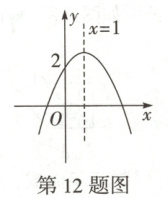
12. 如图，已知抛物线$y = ax^{2} + bx + c(a \neq 0)$的对称轴是直线$x = 1$，且过点$(0, 2)$，顶点在第一象限，其部分图象如图所示. 下列命题中：①$abc ＜ 0$；②$2a + b ＜ -1$；③对于任意实数m，都有$a + b \geq m(am + b)$；④$E(x_{1}, y_{1})$，$F(x_{2}, y_{2})$是抛物线$y = ax^{2} + bx(a \neq 0)$上的两个点，若$x_{1} ＜ x_{2}$，且$x_{1} + x_{2} ＞ 2$，则$y_{1} ＜ y_{2}$. 真命题的序号是(D)

A.①②
B.③④
C.②④
D.①③

答案： 12.D

13. 计算：$3\sqrt{2} ÷ \sqrt{2} = $3.

答案： 13.3

14. 如图，是一组悬挂在天花板上的吊灯，清洗时每次取下一个吊灯，且取吊灯A前必须先取下吊灯B，直到3个吊灯都被取下为止，则清洗时第二个取下的吊灯是A的概率是$\frac{1}{3}$.

答案： 14.$\frac{1}{3}$

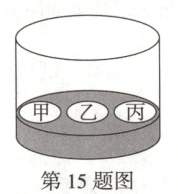
15. 如图，一个圆柱形容器，其底部有三个完全相同的小孔槽，分别命名为甲槽、乙槽、丙槽. 有大小质地完全相同的三个小球，每个小球标有从1至9中选取的一个数字，且每个小球所标数字互不相同. 作如下操作：将这三个小球放入容器中，摇动容器使这三个小球全部落入不同的小孔槽(每个小孔槽只能容下一个小球)，取出小球记录下各小孔槽的计分(分数为落入该小孔槽小球上所标的数字)，完成第一次操作. 再重复以上操作两次. 已知甲槽、乙槽、丙槽三次操作计分之和分别为20分、10分、9分，其中第一次操作计分最高的是乙槽，则第二次操作计分最低的是乙槽.(填“甲槽”“乙槽”或“丙槽”)

答案： 15.乙槽

16. (2025黑白卷)如图，在$\triangle ABC$中，$∠ACB = 90^{\circ}$，$\tan∠ABC = \frac{1}{3}$，$AC = 2$，点P在BC上，$BP = 4$，将BP绕点B顺时针旋转α，得到线段BQ，连接AQ，取AQ的中点M，连接CM. 在BP旋转的过程中，CM长度的最大值为2+$\sqrt{10}$.

答案： 16.2+$\sqrt{10}$