《2026年万唯中考试题研究数学河北专版》

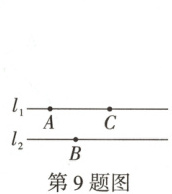
9. 万唯原创 如图，直线$l_{1}// l_{2}$，它们之间的距离为 2，A，C 是直线$l_{1}$上的两个定点，且$AC = 4$，B 是直线$l_{2}$上一动点，在同一平面内找一点 D，使得四边形 ABCD 是平行四边形，当点 D 与点 C 之间的距离最小时，$∠BDC$的度数为(B)

A.$30^{\circ}$
B.$45^{\circ}$
C.$60^{\circ}$
D.$90^{\circ}$

答案： 9. B

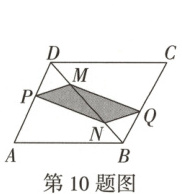
10. 如图，在$□ ABCD$中，$∠A$为锐角，且$AB≠AD$，点 M，N 是 BD 上的点(不与点 B，D 重合)，$DM = BN$，点 P，Q 分别在 AD，BC 上，添加下列条件

不

能

判定四边形 PNQM 是平行四边形的是(A)

A.$PM⊥BD$，$QN⊥BC$
B.$∠DPM = ∠BQN$
C.$PM// AB$，$QN// DC$
D.P，Q 分别是 AD，BC 的中点

答案： 10. A

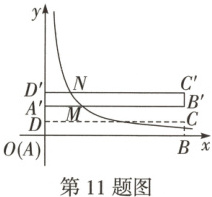
11. 万唯原创 如图，矩形 ABCD 中，点 A 与原点 O 重合，点 B 在 x 轴上，点$D(0,1)$，将矩形 ABCD 沿 y 轴向上平移$a(a＞0)$个单位长度，得到矩形$A'B'C'D'$，边$A'B'$，$C'D'$分别与双曲线$y=\frac{6}{x}(x＞0)$交于点 M，N，若点 M，N 之间的水平距离 d 满足$1≤d≤3$，则 a 的取值范围为(B)

A.$1≤a≤3$
B.$1≤a≤2$
C.$2≤a≤3$
D.$2≤a≤6$

答案： 11. B

12. 万唯原创 如图，在矩形 OABC 中，点$A(4,0)$，点$B(4,2)$，在线段 OA 的四等分点 P(靠近点 O)处有一光点沿与矩形边夹角$45^{\circ}$方向向矩形内弹出，与矩形 OABC 的边撞击后，继续按相同的方式弹射，即光点每次的弹射路线与矩形 OABC 的边所成的角均相等，直至光点第一次回到点 P 停止，则光点第 5 次与矩形 OABC 边的撞击点坐标为(D)

A.$(3,2)$或$(1,2)$
B.$(0,2)$或$(4,1)$
C.$(3,1)$或$(2,2)$
D.$(3,2)$或$(0,1)$

答案： 12. D

13. 新考法 条件开放 若$\sqrt{2 - x}$在实数范围内有意义，请写出一个满足条件的 x 的正整数值为1。

答案： 13. 1（或2）

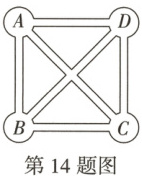
14. 某校的科技兴趣小组开发了一款机器狗小游戏，具体如下：如图，在一个正方形 ABCD 中，设 A 点为机器狗的起点，机器狗每次只能从一个顶点移动到另一个顶点(机器狗不会返回前一个顶点)，则机器狗从起点开始随机运行 2 次后恰好停在 C 点的概率为$\frac{1}{3}$。

答案： $14. \frac{1}{3}$

15. 若$n(n + 1) = 5$，则$(n + 1)(n - 1) + n(n + 2) =$9。

答案： 15. 9

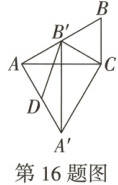
16. 如图，在$Rt\triangle ABC$中，$∠ACB = 90^{\circ}$，$∠B = 60^{\circ}$，$BC = 2$，将$\triangle ABC$绕点 C 逆时针旋转得到$\triangle A'B'C$，且$B'$恰好落在 AB 上，连接$AA'$，取$AA'$的中点 D，连接$B'D$，则$B'D$的值为\sqrt{7}。

答案： $16. \sqrt{7}$