第17页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
1. 实数a在数轴上的对应点的位置如图所示,则它的相反数可能是(

A.1.5
B.2.5
C.-1.5
D.-2.5
A
)
A.1.5
B.2.5
C.-1.5
D.-2.5
答案:
1. A
2. 如图是由3个相同的小正方形组成的图形,若再补画一个相同的小正方形,使补画后的图形是轴对称图形,则补画方法一共有(
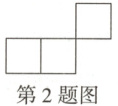
A.2种
B.3种
C.4种
D.5种
C
)
A.2种
B.3种
C.4种
D.5种
答案:
2. C
3. (2025黑白卷)下列运算中,正确的是(
A.$x^2· x = 2x^3$
B.$7x - 4x = 3$
C.$(2x + y)(2x - y) = 4x^2 - y^2$
D.$(x^2y)^3 = x^2y^3$
C
)A.$x^2· x = 2x^3$
B.$7x - 4x = 3$
C.$(2x + y)(2x - y) = 4x^2 - y^2$
D.$(x^2y)^3 = x^2y^3$
答案:
3. C
4. 当$x = \pm 2$时,分式$\frac{x - 1}{□}$无意义,则□所表示的代数式可能是(
A.$x - 2$
B.$x + 2$
C.$2x^2 - 8$
D.$x(x + 2)$
C
)A.$x - 2$
B.$x + 2$
C.$2x^2 - 8$
D.$x(x + 2)$
答案:
4. C
5. 万唯原创 小李在计算$2023^{2023} - 2023^{2021}$时,发现其计算结果能被三个连续整数整除,则这三个整数是(
A.2023,2024,2025
B.2022,2023,2024
C.2021,2022,2023
D.2020,2021,2022
B
)A.2023,2024,2025
B.2022,2023,2024
C.2021,2022,2023
D.2020,2021,2022
答案:
5. B
6. (2025黑白卷)如图,将$\triangle ABC$折叠,使点A,B重合,折痕为DE,连接BE.
甲:能够比较$\angle A$与$\angle ABC$的大小.
乙:能够比较AC与BC的长短.
下列判断正确的是(
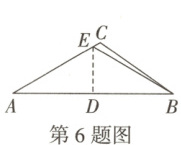
A.甲、乙的说法都正确
B.甲、乙的说法都不正确
C.甲的说法正确,乙的说法不正确
D.甲的说法不正确,乙的说法正确
甲:能够比较$\angle A$与$\angle ABC$的大小.
乙:能够比较AC与BC的长短.
下列判断正确的是(
A
)
A.甲、乙的说法都正确
B.甲、乙的说法都不正确
C.甲的说法正确,乙的说法不正确
D.甲的说法不正确,乙的说法正确
答案:
6. A
7. 已知$(\sqrt{2} + \sqrt{3})^2 = 5 + 2\sqrt{a}$,则a的值为(
A.2
B.3
C.5
D.6
D
)A.2
B.3
C.5
D.6
答案:
7. D
8. 如图,在正方形网格中,A,B,C,D均为格点,若以其中一点为坐标原点,以互相垂直的网格线所在直线为坐标轴,建立平面直角坐标系,使其余三个点中存在两个点关于一条坐标轴对称,则坐标原点应选(
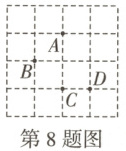
A.点A
B.点B
C.点C
D.点D
B
)
A.点A
B.点B
C.点C
D.点D
答案:
8. B
9. (2025定心卷)如图,$AD = BC$,$AD// BC$,AC交BD于点P,E,F分别是AD,DC的中点,选择图中的四个点为顶点画四边形,其中能画出的平行四边形有(
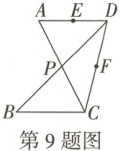
A.2个
B.3个
C.4个
D.5个
C
)
A.2个
B.3个
C.4个
D.5个
答案:
9. C
查看更多完整答案,请扫码查看


