第6页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
9. 万唯原创 有 $ a,b $ 两根小棒如图所示,现要将 $ a,b $ 两根小棒中的一根剪成两段与另外一根围成三角形,那么下面剪法中,一定能围成三角形的是 (
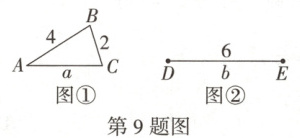
A.$ a $ 小棒任意剪一刀
B.$ b $ 小棒任意剪一刀
C.$ a $ 小棒正中间剪一刀
D.$ b $ 小棒正中间剪一刀
D
)
A.$ a $ 小棒任意剪一刀
B.$ b $ 小棒任意剪一刀
C.$ a $ 小棒正中间剪一刀
D.$ b $ 小棒正中间剪一刀
答案:
9.D
10. (2025 黑白卷)如图,在四边形 $ ABCD $ 中, $ E $ 是 $ AB $ 延长线上一点,已知 $ ∠CBE = 42° $. 嘉嘉认为: $ ∠DAB = ∠DCB = 42° $ 时,四边形 $ ABCD $ 是平行四边形;淇淇认为: $ ∠ADC = 138° $ 时,四边形 $ ABCD $ 为平行四边形. 则下列说法正确的是 (
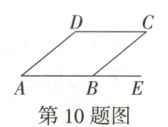
A.淇淇对,嘉嘉不对
B.嘉嘉对,淇淇不对
C.两人都对
D.两人都不对
B
)
A.淇淇对,嘉嘉不对
B.嘉嘉对,淇淇不对
C.两人都对
D.两人都不对
答案:
10.B
11. 万唯原创 某数学老师在课外活动课上做了一个有趣的游戏,他在卡片上写出了一个各个数位数字之和为 8 且个位数字不为零的三位数 $ M $,并让同学完成了以下计算:第一步,将 $ M $ 的百位数字与个位数字对调后得到新的三位数 $ N $;第二步,$ N $ 减去 $ M $ 的个位数字的 4 倍得到 $ S $;若 $ S $ 能被 8 整除,则 $ M $ 的最小值为 (
A.116
B.233
C.422
D.611
B
)A.116
B.233
C.422
D.611
答案:
11.B
12. (2025 样卷)如图,正方形 $ ABCD $ 的顶点坐标分别为 $ A(-2,4),B(-2,-1),C(3,-1) $. 抛物线经过点 $ D $,顶点坐标为 $ (1,0) $,将此抛物线在正方形 $ ABCD $ 内(含边界)的部分记为图象 $ G $. 若直线 $ y = kx - 2k + 2(k ≠ 0) $ 与图象 $ G $ 有唯一交点,则 $ k $ 的取值范围是 (
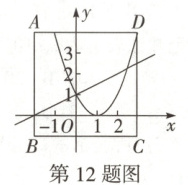
A.$ k > 2 $ 或 $ k < -\frac{2}{3} $
B.$ -\frac{2}{3} < k < 0 $ 或 $ 0 < k < 2 $
C.$ k > 1 $ 或 $ k < -3 $
D.$ k > 1 $ 或 $ k < -3 $ 或 $ k = -2 $
A
)
A.$ k > 2 $ 或 $ k < -\frac{2}{3} $
B.$ -\frac{2}{3} < k < 0 $ 或 $ 0 < k < 2 $
C.$ k > 1 $ 或 $ k < -3 $
D.$ k > 1 $ 或 $ k < -3 $ 或 $ k = -2 $
答案:
12.A
13. (2025 样卷)计算 $ \sqrt{18} - \sqrt{2} = $
2\sqrt{2}
.
答案:
$13.2\sqrt{2}$
14. 万唯原创 将一个矩形分割成 $ A,B,C,D,E $ 五个区域,用红、黄、蓝、绿四种不同的颜色分别给这五个区域着色,已着色情况如图所示,若给 $ E $ 区域着色后(颜色可重复使用),使每相邻两个区域的着色都不相同的概率为
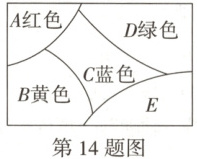
\frac{1}{4}
.
答案:
$14.\frac{1}{4}$
15. 万唯原创 对于实数 $ m,n $,定义一种新运算:$ m★n = m(m - n) $,若关于 $ x $ 的方程 $ x★2 = k $($ k $ 为正整数)有实数根,则 $ k $ 的最小值为
1
.
答案:
15.1
16. 万唯原创 如图,在边长为 5 的正方形 $ ABCD $ 中,连接 $ AC,AE $ 平分 $ ∠CAD $,交边 $ CD $ 于点 $ E,F $ 为线段 $ AE $ 上一点,连接 $ BF,CF $,则 $ △BCF $ 周长的最小值为
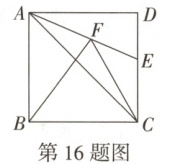
5\sqrt{3}+5
.
答案:
$16.5\sqrt{3}+5$
查看更多完整答案,请扫码查看


