《2026年万唯中考试题研究数学河北专版》

9. (2025黑白卷)课堂上,老师出示了这样一个问题:如图①,已知 $ \angle PAB = 45° $,请利用尺规作 $ \angle CPA = 135° $.如图②是甲、乙、丙三名同学的作法,则其中正确的是

A.甲、乙正确,丙错误
B.乙、丙正确,甲错误
C.甲、丙正确,乙错误
D.甲、乙、丙均正确

答案： 9.D

10. (2025定心卷)如图,已知一次函数 $ y_1 = 2x + 4 $ 的图象与 $ x $ 轴交于点 $ A $,与 $ y $ 轴交于点 $ B $,且点 $ A $ 关于 $ y $ 轴的对称点为 $ C $.一次函数 $ y_2 = kx + b $ 的图象经过点 $ B $, $ D $,且点 $ D $ 在 $ x $ 轴上,当线段 $ CD ＜ 1 $ 时, $ k $ 的取值范围为

A.$ -4 ＜ k $
B.$ -4 \leq k \leq -\frac{4}{3} $
C.$ -4 ＜ k ＜ -\frac{4}{3} $
D.$ k ＜ -\frac{4}{3} $
[img]

答案： 10.C

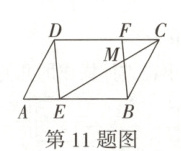
11. 万唯原创 如图,在 $ □ ABCD $ 中,点 $ E $, $ F $ 分别在边 $ AB $, $ CD $ 上,且 $ AB = 3AE $, $ CD = 3CF $,连接 $ DE $, $ BF $, $ CE $, $ BF $ 与 $ CE $ 交于点 $ M $.若 $ DE = 6 $,则 $ BM $ 的长为

A.2
B.3
C.4
D.$ \frac{9}{2} $
[img]

答案： 11.C

12. “约瑟夫环”是一个经典的数学问题,生活中常利用“约瑟夫环”的基本原理做游戏,游戏过程如下: $ n $ 个人围成一圈,从第1个人开始报数,数到 $ m $ 的人出列,然后从出列的下一个人重新开始报数,数到 $ m $ 的人再出列,如此循环,直到所有人都出列为止,问题是确定最后出列的那个人在最初的圆圈中的位置.若现在有5个小朋友做这个游戏,依次编号为1~5,规定数到3的小朋友就退出游戏,那么最后一个退出游戏的小朋友的编号为

A.2
B.3
C.4
D.5

答案： 12.C

13. $ 1.37 × 10^n $ 是一个精确到百万位的整数,则 $ n $ 的值为8.

答案： 13.8

14. 如图,点 $ M(m, 0) $, $ N(m, 6) $ 分别是线段 $ MN $ 的两个端点,其中 $ m ＞ 0 $.反比例函数 $ G: y = \frac{k}{x}(k ＞ 0) $ 的图象经过点 $ (2, 6) $,并交线段 $ MN $ 于点 $ P $.若 $ MP = NP $,则 $ m $ 的值为4.
[img]

答案： 14.4

15. 某校组织多项活动加强科学教育,八年级(一)班分两批次确定项目组成员,参加“实践探究”活动,第一批次确定了7人,第二批次确定了1名男生、2名女生.现从项目组中随机抽取1人承担联络任务,若抽中男生的概率为 $ \frac{3}{5} $,则第一批次确定的人员中,男生为5人.

答案： 15.5

16. 万唯原创 如图, $ O $ 是边长为2的正六边形 $ ABCDEF $ 的中心,以 $ AB $ 为边在正六边形 $ ABCDEF $ 的内部作正方形 $ ABMN $,则点 $ M $ 到直线 $ OD $ 的距离为\sqrt{3}-1.
[img]

答案： $16.\sqrt{3}-1$