第55页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
17. (8 分)万唯原创 如图,在单位长度为 1 的数轴上有 $ A $,$ B $,$ C $,$ D $,$ E $,$ F $ 六个点,相邻两点之间的距离均为 $ n $($ n $ 为正整数),点 $ B $ 表示的数为 -2。
(1)若 $ n = 2 $,则表示原点的是点
(2)若点 $ E $ 所表示的数是 10,求 $ n $ 的值及点 $ D $ 所表示的数。
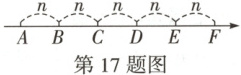
(1)若 $ n = 2 $,则表示原点的是点
C
,点 $ E $ 所表示的数是4
;(2)若点 $ E $ 所表示的数是 10,求 $ n $ 的值及点 $ D $ 所表示的数。

答案:
17.
(1)C;4;
(2)$n = 4$,点$D$所表示的数为$6$.
(1)C;4;
(2)$n = 4$,点$D$所表示的数为$6$.
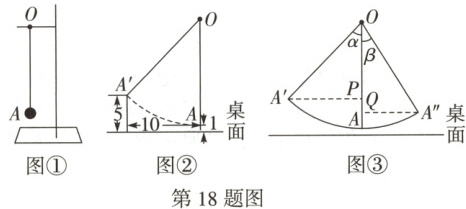
18. (8 分)(2025 黑白卷)综合与实践
【主题】模拟单摆实验。
【工具】
嘉嘉同学在物理课上学习了发声物体的振动实验后,对其做了进一步的探究,准备了如下工具:一个带横杆的支架,一条摆绳,一个小球,量尺,量角器…
【操作】
步骤 1:将一个小球 $ A $ 用摆绳挂在一个支架的横杆点 $ O $ 处,则小球 $ A $ 可以自由摆动,如图①,$ OA $ 表示小球静止时的位置,此时量得小球 $ A $ 距桌面为 1 cm;
步骤 2:如图②,当嘉嘉用发声物体靠近小球时,小球从 $ OA $ 摆到 $ OA' $ 位置,量得此时小球往前推进的水平距离为 10 cm,小球距桌面 5 cm;
步骤 3:如图③,将小球从与竖直方向夹角为 $ \alpha $ 的位置 $ OA' $ 自由释放,摆动到另一侧与竖直方向夹角为 $ \beta $ 的 $ OA'' $ 位置,记录两次位置的高度差 $ PQ = h $ cm。
(以上步骤中,小球大小忽略不计,摆绳 $ OA $ 紧绷,且长度不变)
【探索】
(1)请你根据嘉嘉步骤 1 和步骤 2 所记录的数据,推算出摆绳 $ OA $ 的长度;
(2)根据上述步骤,写出摆绳 $ OA $ 和 $ \alpha $,$ \beta $,$ h $ 之间的关系式。
【主题】模拟单摆实验。
【工具】
嘉嘉同学在物理课上学习了发声物体的振动实验后,对其做了进一步的探究,准备了如下工具:一个带横杆的支架,一条摆绳,一个小球,量尺,量角器…
【操作】
步骤 1:将一个小球 $ A $ 用摆绳挂在一个支架的横杆点 $ O $ 处,则小球 $ A $ 可以自由摆动,如图①,$ OA $ 表示小球静止时的位置,此时量得小球 $ A $ 距桌面为 1 cm;
步骤 2:如图②,当嘉嘉用发声物体靠近小球时,小球从 $ OA $ 摆到 $ OA' $ 位置,量得此时小球往前推进的水平距离为 10 cm,小球距桌面 5 cm;
步骤 3:如图③,将小球从与竖直方向夹角为 $ \alpha $ 的位置 $ OA' $ 自由释放,摆动到另一侧与竖直方向夹角为 $ \beta $ 的 $ OA'' $ 位置,记录两次位置的高度差 $ PQ = h $ cm。
(以上步骤中,小球大小忽略不计,摆绳 $ OA $ 紧绷,且长度不变)
【探索】
(1)请你根据嘉嘉步骤 1 和步骤 2 所记录的数据,推算出摆绳 $ OA $ 的长度;
(2)根据上述步骤,写出摆绳 $ OA $ 和 $ \alpha $,$ \beta $,$ h $ 之间的关系式。

答案:
18.
(1)摆绳$OA$的长度为$14.5$ $cm$;
(2)$OA = \frac{h}{\cos \beta - \cos \alpha}$
(1)摆绳$OA$的长度为$14.5$ $cm$;
(2)$OA = \frac{h}{\cos \beta - \cos \alpha}$
查看更多完整答案,请扫码查看


