《2026年万唯中考试题研究数学河北专版》

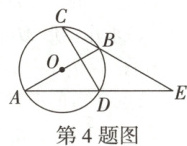
4.(8分)如图,$AB$是$\odot O$的直径,$CD$是$\odot O$的弦,且$\overset{\frown}{CB}=\overset{\frown}{BD}$,连接$AD$并延长,与$CB$的延长线交于点$E$,且$\angle E=\angle DCE$.
(1)求证:$D$是$AE$的中点;
(2)若$DE=4$,求$\overset{\frown}{AD}$的长.

答案：
4.
(1)证明:如解图,连接AC.
∵AB是⊙O的直径,
∴∠ACE = 90°,
∴∠ACD + ∠DCE = ∠E + ∠CAD = 90°.
∵∠E = ∠DCE,
∴∠ACD = ∠CAD,CD = ED,
∴AD = CD = ED,
∴D是AE的中点;

(2)解:如解图,连接OD.
∵AB是⊙O的直径,$\widehat{CB}=\widehat{BD}$,
∴AB垂直平分CD,
∴AC = AD.
又
∵AD = CD,
∴AC = AD = CD,
∴△ACD是等边三角形,
∴∠ACD = 60°,
∴∠AOD = 120°.
过点O作AD的垂线,垂足为M,
∴∠AOM = $\frac{1}{2}$∠AOD = 60°.
∵DE = 4,
∴AD = 4,
∴AM = $\frac{1}{2}$AD = 2.
在Rt△AOM中,sin∠AOM = $\frac{AM}{AO}$,
∴AO = $\frac{2}{\frac{\sqrt{3}}{2}}$ = $\frac{4\sqrt{3}}{3}$,
∴$\overset\frown{AD}$的长为$\frac{120\pi×\frac{4\sqrt{3}}{3}}{180}=\frac{8\sqrt{3}}{9}\pi$.

5.(8分)$万唯原创$如图,抛物线$y=ax^2+bx-3$与$x$轴交于$A,B$两点(点$A$在点$B$的左侧),对称轴为直线$x=2$,$(3,-\frac{15}{4})$是抛物线上一点.
(1)求抛物线的函数解析式;
(2)已知当$-2\leq x\leq q$时,抛物线对应函数的最小值与最大值之和为$1$,求$q$的值.

答案： 5.解:
(1)抛物线的函数解析式为y = $\frac{1}{4}x^{2}-x-3$;
(2)由
(1)知,抛物线的函数解析式为y = $\frac{1}{4}x^{2}-x-3$,
令y = 0,即$\frac{1}{4}x^{2}-x-3 = 0$,解得$x_1$ = -2,$x_2$ = 6,
∴A(-2,0),B(6,0).
∵抛物线开口向上,抛物线对称轴为直线x = 2,
∴当-2 ≤ x ≤ 6时,抛物线对应函数的函数值均不为正数.
∵当-2 ≤ x ≤ q时,抛物线对应函数的最小值与最大值之和为1,
∴q ＞ 6,
将x = 2代入y = $\frac{1}{4}x^{2}-x-3$,得y = -4,即最小值为y = -4,
∴最大值为1 - (-4) = 5,
令y = 5,即$\frac{1}{4}x^{2}-x-3 = 5$,解得x = -4(舍去)或x = 8,
∴q的值为8.
(开封·河南模拟)参考答案