第14页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
8. 如图是化简“$\frac{a + 2}{a^{2}+3a}÷(\frac{-2}{a + 3}-a)$”的部分解题步骤,则“”上可以填 (

A.$\frac{-2}{a + 3}-\frac{a + 2}{a(a + 3)}÷\frac{a(a + 3)}{a + 3}$
B.$\frac{-2 - a^{2}-3a}{a + 3}$
C.$\frac{-2 - a^{2}+3a}{a + 3}$
D.$\frac{1 - a^{2}}{a + 3}$
B
)
A.$\frac{-2}{a + 3}-\frac{a + 2}{a(a + 3)}÷\frac{a(a + 3)}{a + 3}$
B.$\frac{-2 - a^{2}-3a}{a + 3}$
C.$\frac{-2 - a^{2}+3a}{a + 3}$
D.$\frac{1 - a^{2}}{a + 3}$
答案:
B
9. 当三角形面积一定时,它的底边长$a(cm)$与底边上的高$h(cm)$成反比例函数关系,其图象如图所示,则当底边长$a(cm)$满足$1.2 < a < 2.4$时,底边上的高$h(cm)$的取值范围是 (

A.$5 < h < 10$
B.$1 < h < 2$
C.$0.5 < h < 1$
D.$0.1 < h < 0.2$
A
)
A.$5 < h < 10$
B.$1 < h < 2$
C.$0.5 < h < 1$
D.$0.1 < h < 0.2$
答案:
A
10. 万唯原创 如图,$\odot O$的内接正六边形$ABCDEF$的面积为$54\sqrt{3}$,$GH$为$\odot O$的直径,且点$G,H$分别为$\overset{\frown}{CD},\overset{\frown}{AF}$的中点,若以点$E$为圆心,$4\sqrt{3}$长为半径画弧,与$GH$相交于点$M$,则$\angle GEM$的度数为 (
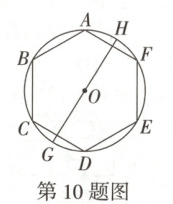
A.$15^{\circ}$
B.$75^{\circ}$
C.$15^{\circ}$或$75^{\circ}$
D.$30^{\circ}$或$60^{\circ}$
C
)
A.$15^{\circ}$
B.$75^{\circ}$
C.$15^{\circ}$或$75^{\circ}$
D.$30^{\circ}$或$60^{\circ}$
答案:
C
11. 在平面直角坐标系中,点$A$的坐标为$(-3,m + 2)$,点$B$的坐标为$(-1,m - 4)$,且$A,B$两点在直线$AB$上.若点$C(t + 1,n_{1})$和点$D(t - 2,n_{2})$也在直线$AB$上,则$n_{1}-n_{2}$的值为 (
A.$-9$
B.$-3$
C.6
D.9
A
)A.$-9$
B.$-3$
C.6
D.9
答案:
A
12. 万唯原创 如图,在$Rt\triangle ABC$中,$\angle ABC = 90^{\circ}$,点$D$为$BC$上一点,且$BD = AB$,连接$AD,BE\perp AC$于点$E$,将$BE$绕点$B$逆时针旋转$90^{\circ}$得到线段$BF$,连接$EF$交$AD$于点$G$,若$AB = 6$,则$DG$的长为(
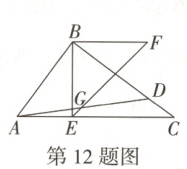
A.$\sqrt{2}$
B.$3\sqrt{2}$
C.$6\sqrt{2}$
D.8
B
)
A.$\sqrt{2}$
B.$3\sqrt{2}$
C.$6\sqrt{2}$
D.8
答案:
B
13. 万唯原创 嘉嘉的妈妈利用下班业余时间在小区摆地摊,嘉嘉对某一周7天的收入数据进行分析,并列出方差公式:$s^{2}=\frac{1}{7}[(80 - x)^{2}+(60 - x)^{2}+(90 - x)^{2}×3+(110 - x)^{2}×2]$,则该周的平均收入为
90
元.
答案:
90
14. 若$(2x - m)(x + 1)$的运算结果是关于$x$的二次二项式,则$m$的值等于
0或2
.
答案:
0或2
15. 万唯原创 如图,嘉嘉用四个全等的直角三角形拼接了一个“赵爽弦图”,其中小正方形$EFGH$的面积为1. 连接$AC$,交$BG$于点$P$,交$DE$于点$M$,则$S_{\triangle AEP}-S_{\triangle CGP}=$
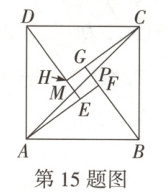
\frac{1}{2}
.
答案:
$\frac{1}{2}$
16. 万唯原创 某校七年级举办的趣味运动会,共设计了五个比赛项目,每个项目都以班级为单位参赛,且每个班级都需要参加全部项目.规定:每项比赛中,只有排在前三名的班级记成绩(没有并列班级),第一名的班级记$a$分,第二名的班级记$b$分,第三名的班级记$c$分($a > b > c,a,b,c$均为正整数);各班比赛的总成绩为本班每项比赛的记分之和.该年级共有四个班,若这四个班比赛的总成绩分别为$21,6,9,4$,则$abc$的值为
10
.
答案:
10
查看更多完整答案,请扫码查看


