《2026年万唯中考试题研究数学河北专版》

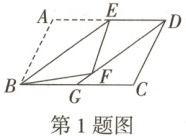
1. 如图,在平行四边形 $ABCD$ 中,点 $E$ 为 $AD$ 边的中点,将 $\triangle ABE$ 沿 $BE$ 翻折,得到 $\triangle FBE$,连接 $DF$ 并延长交 $BC$ 于点 $G$,若 $BE = AD = 3$,平行四边形 $ABCD$ 的面积为 $6$,则 $FG$ 的长为 (C)

A.$\sqrt{3}$
B.$2$
C.$3-\sqrt{5}$
D.$\sqrt{5}-1$

答案： C

2. (2025 黑白卷)任取一个正整数,若是奇数,就将该数乘 $3$ 再加上 $1$;若是偶数,就将该数除以 $2$. 如果某个正整数通过上述变换能变成 $1$,我们就把第一次变成 $1$ 时所经过的变换次数称为它的路径长,如:取正整数 $5$,根据上述运算法则得出 $5→16→8→4→2→1$,则路径长为 $5$. 若正整数 $m$ 的路径长为 $n$,则 $m$ 的最大值为 (D)

A.$2^{m}$
B.$2^{m - 1}$
C.$2^{n - 1}$
D.$2^{n}$

答案： D

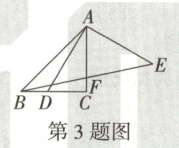
3. 万唯原创 如图,在等腰 $Rt\triangle ABC$ 中,$AC = BC = 3$,$D$ 是 $BC$ 上一点,连接 $AD$,$\angle BAD = 15^{\circ}$,过点 $A$ 作 $AE\perp DA$ 且 $AE = AD$,连接 $BE$ 交 $AC$ 于点 $F$,则 $CF$ 的长为\frac{3-\sqrt{3}}{2}.

答案： $\frac{3-\sqrt{3}}{2}$

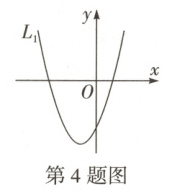
4. (2025 定心卷)如图,已知抛物线 $L_{1}:y = ax^{2}+2ax - 3$ 经过点 $A(2,5)$,平移抛物线 $L_{1}$,使其顶点在直线 $y = -2x + 6$ 上,得到抛物线 $L_{2}$.
(1)求抛物线 $L_{1}$ 的顶点坐标;
(2)若抛物线 $L_{2}$ 的顶点关于坐标原点 $O$ 的对称点在抛物线 $L_{1}$ 上,求抛物线 $L_{2}$ 的解析式;
(3)若点 $M(6 - t,m)$,$N(t - 3,n)$ 在抛物线 $L_{2}$ 上,当 $t＞\frac{9}{2}$ 时,都有 $m\geq n$,求抛物线 $L_{2}$ 顶点纵坐标的最大值.
二次函数最值问题

答案： 4. 解：
(1)抛物线$L_1$的顶点坐标为$(-1,-4)$；
(2)设$L_2$的顶点的横坐标为$h$.
$\because L_2$的顶点在直线$y=-2x+6$上，
$\therefore L_2$的顶点坐标为$(h,-2h+6)$，
$\therefore L_2$的解析式为$y=(x-h)^2-2h+6$.
$\because$点$(h,-2h+6)$关于坐标原点$O$的对称点为$(-h,2h-6)$，
将点$(-h,2h-6)$的坐标代入$y=(x+1)^2-4$，得$(-h+1)^2-4=2h-6$，
整理得$h^2-4h+3=0$，
解得$h_1=1,h_2=3$；
$\therefore$抛物线$L_2$的解析式为$y=(x-1)^2+4$或$y=(x-3)^2$；
(3)由
(2)可设抛物线$L_2$的解析式为$y=(x-h)^2-2h+6$.
$\because$点$M(6-t,m),N(t-3,n)$在抛物线$L_2$上，
$\therefore m=(6-t-h)^2-2h+6,n=(t-3-h)^2-2h+6$，
$\therefore m-n=(6-t-h)^2-(t-3-h)^2=[(6-t-h)+(t-3-h)][(6-t-h)-(t-3-h)]=(3-2h)(9-2t)$.
$\because m\geq n$，
$\therefore m-n=(3-2h)(9-2t)\geq0$.
$\because t＞\frac{9}{2},\therefore9-2t＜0$，
$\therefore3-2h\leq0$，
$\therefore h\geq\frac{3}{2}$，
由
(2)知$L_2$的顶点的纵坐标为$-2h+6$，且$-2h+6$随$h$的增大而减小，
$\therefore$当$h=\frac{3}{2}$时，$-2h+6$取最大值，最大值为$-2×\frac{3}{2}+6=3$，
$\therefore$抛物线$L_2$顶点纵坐标的最大值为3.