第18页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
10. 甲、乙、丙三人进行乒乓球单打训练,每局两人进行比赛,第三个人做裁判,每一局都要分出胜负,胜方和原来的裁判进行新一局的比赛,输方转做裁判,依次进行. 半天训练结束时,发现甲共当裁判4局,乙、丙分别打了9局、14局比赛,在这半天的训练中,第7局比赛的裁判是(
A.甲
B.乙
C.丙
D.无法确定
B
)A.甲
B.乙
C.丙
D.无法确定
答案:
10. B
11. 万唯原创 新定义:若一个点的横坐标与纵坐标之和为0,则称这个点为“互异点”,若抛物线$y = x^2 - 4x + c$(c为常数)在$-1 < x < 4$上存在两个“互异点”,则c的取值范围是(
A.$\frac{9}{4} < c < 4$
B.$-4 < c < \frac{9}{4}$
C.$-4 < c < 4$
D.$0 < c < \frac{9}{4}$
B
)A.$\frac{9}{4} < c < 4$
B.$-4 < c < \frac{9}{4}$
C.$-4 < c < 4$
D.$0 < c < \frac{9}{4}$
答案:
11. B
12. (2025定心卷)将图①中的矩形和正方形纸片沿图②中的虚线剪成5块,再用这5块拼接成如图③所示矩形结构的“弦图”,其中阴影部分为空余部分,设图①中矩形长和宽分别为5a,4a,正方形边长为2b,若图③中$CG = 2CE$,则$\frac{b}{a}$的值为(
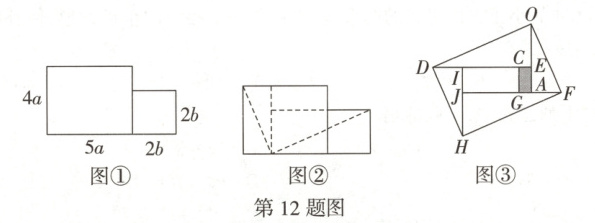
A.$\frac{15 - \sqrt{57}}{6}$
B.$\frac{6}{5}$
C.$\frac{15 + \sqrt{57}}{8}$
D.$\frac{5}{2}$
A
)
A.$\frac{15 - \sqrt{57}}{6}$
B.$\frac{6}{5}$
C.$\frac{15 + \sqrt{57}}{8}$
D.$\frac{5}{2}$
答案:
12. A
13. 藤球是一项古老而独特的体育运动项目,有着悠久的历史,又叫“脚踢的排球”. 下表是学校藤球队中三名学生五次传踢球成绩的平均数及方差统计表,若要从这三名学生中选择一名成绩好且稳定的学生作为校藤球队的队长,则应选择学生
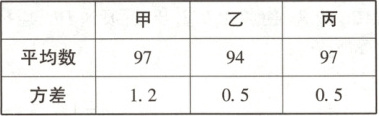
丙
.
答案:
13. 丙
14. 万唯原创 在边长分别为a,b的大矩形草坪内修建一个小矩形花坛,小矩形花坛各边到大矩形草坪各边的距离如图所示,则小矩形花坛的面积是
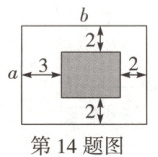
ab - 5a - 4b + 20
.(用含a,b的代数式表示)
答案:
14. ab - 5a - 4b + 20
15. 万唯原创 如图,在$\triangle ABC$中,$\angle ACB = 90°$,$AC = BC$,点M是AC上的一点,过点M作$MN// AB$交BC于点N,将$\triangle CMN$绕点C按逆时针方向旋转$\alpha(0° < \alpha < 180°)$得到$\triangle CDE$,连接AD,BE,若$AD = \sqrt{5}$,则BE的长为.
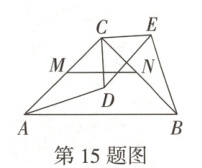

答案:
$15. \sqrt{5}$
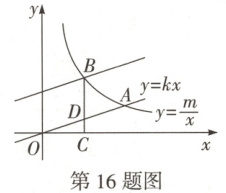
16. (2025定心卷)如图,直线$y = kx$与反比例函数$y = \frac{m}{x}(m > 0,x > 0)$的图象相交于点A,将直线$y = kx$向上平移3个单位长度与反比例函数$y = \frac{m}{x}(m > 0,x > 0)$的图象相交于点B,$BC\perp x$轴于点C,交OA于点D,$OD = AD$,若$OC = 3$,则m的值为
12
.
答案:
16. 12
查看更多完整答案,请扫码查看


