《2026年万唯中考试题研究数学河北专版》

17. 新考法 注重过程性学习 （8分）下面是小明同学进行分式化简的过程，请认真阅读并完成相应任务.
分式化简：$\frac{x^{2} - 1}{x^{2} + 2x + 1} - \frac{2x + 1}{2x + 2}$.
解：原式$= \frac{(x + 1)(x - 1)}{(x + 1)^{2}} - \frac{2x + 1}{2(x + 1)}$ ……………………………………………………………………… 第一步
$= \frac{x - 1}{x + 1} - \frac{2x + 1}{2(x + 1)}$ ……………………………………………………………………… 第二步
$= \frac{2(x - 1)}{2(x + 1)} - \frac{2x + 1}{2(x + 1)}$ ……………………………………………………………………… 第三步
$= \frac{2x - 2 - (2x + 1)}{2(x + 1)}$ ……………………………………………………………………… 第四步
$= \frac{2x - 2 - 2x + 1}{2(x + 1)}$ ……………………………………………………………………… 第五步
$= -\frac{1}{2x + 2}$. ……………………………………………………………………… 第六步
任务：
（1）小明的解题过程是从第五步开始错误的，错误的原因是括号前是负号，去括号时，括号里的第二项没有变号；
（2）请写出正确的解题过程.

答案： $(1)$ 分析错误步骤
小明的解题过程是从第五步开始错误的，错误的原因是括号前是负号，去括号时，括号里的第二项没有变号。
$(2)$ 正确解题过程
解：原式$=\frac{(x + 1)(x - 1)}{(x + 1)^{2}} - \frac{2x + 1}{2(x + 1)}$
$=\frac{x - 1}{x + 1} - \frac{2x + 1}{2(x + 1)}$
$=\frac{2(x - 1)}{2(x + 1)} - \frac{2x + 1}{2(x + 1)}$
$=\frac{2x - 2-(2x + 1)}{2(x + 1)}$
$=\frac{2x - 2 - 2x - 1}{2(x + 1)}$
$=\frac{-3}{2(x + 1)}$
$=-\frac{3}{2x + 2}$
综上，答案依次为：$(1)$ 五；括号前是负号，去括号时，括号里的第二项没有变号；$(2)$ 原式$=\frac{(x + 1)(x - 1)}{(x + 1)^{2}} - \frac{2x + 1}{2(x + 1)}=\frac{x - 1}{x + 1} - \frac{2x + 1}{2(x + 1)}=\frac{2(x - 1)}{2(x + 1)} - \frac{2x + 1}{2(x + 1)}=\frac{2x - 2-(2x + 1)}{2(x + 1)}=\frac{2x - 2 - 2x - 1}{2(x + 1)}=\frac{-3}{2(x + 1)}=-\frac{3}{2x + 2}$ 。

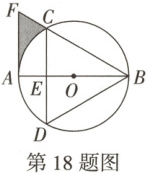
18. （8分）万唯原创 如图，$AB$是$\odot O$的直径，弦$CD$与$AB$交于点$E$，且$\overset{\frown}{AC} = \overset{\frown}{AD}$，连接$BC$，$BD$，$BD = CD$，过点$A$作$\odot O$的切线，与$BC$的延长线交于点$F$.
（1）求证：$\angle D = \angle F$；
（2）若$\odot O$的半径为6，求阴影部分的面积（结果保留$\pi$）.

答案：

(1)证明略;
(2)解:由
(1)得,$\angle D=\angle F$,$BD=BC$.
　　$\because BD=CD$,
　　$\therefore \triangle BCD$是等边三角形，
　　$\therefore \angle D=\angle F=\angle DCB=60^{\circ}$.
　　如解图，连接$OC$.
　　$\because OC=OB$,
　　$\therefore \angle OBC=\angle OCB=30^{\circ}$,
　　$\therefore \angle OCE=30^{\circ}$.
　　在$Rt\triangle CEO$中,$CO=6$,$\angle CEO=90^{\circ}$,
　　$\therefore CE=OC·\cos30^{\circ}=3\sqrt{3}$,
　　$\therefore S_{\triangle BCO}=\frac{1}{2}OB· CE=9\sqrt{3}$.
　　在$Rt\triangle ABF$中,$\angle F=60^{\circ}$,$AB=12$,
　　$\therefore AF=\frac{AB}{\tan60^{\circ}}=4\sqrt{3}$,
　　$\therefore S_{\triangle ABF}=\frac{1}{2}AF· AB=24\sqrt{3}$.
　　$\because S_{扇形AOC}=\frac{60\pi×6^{2}}{360}=6\pi$,
　　$\therefore S_{阴影}=S_{\triangle ABF}-S_{\triangle BCO}-S_{扇形AOC}=15\sqrt{3}-6\pi$.