第9页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
8. [2023·包头中考改编]从上面看由几个大小相同的小立方块搭成的几何体,看到的形状图如图所示,其中小正方形中的数字表示在该位置的小立方块的个数,则该几何体从正面看到的形状图是(
]
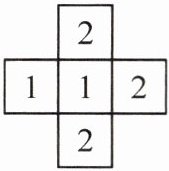
D
)]


答案:
D
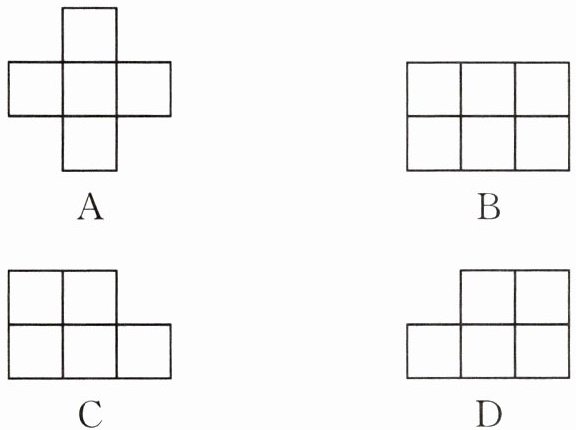
9. 通过小颖和小刚的对话,我们可以判断他们共同搭的几何体是(
]
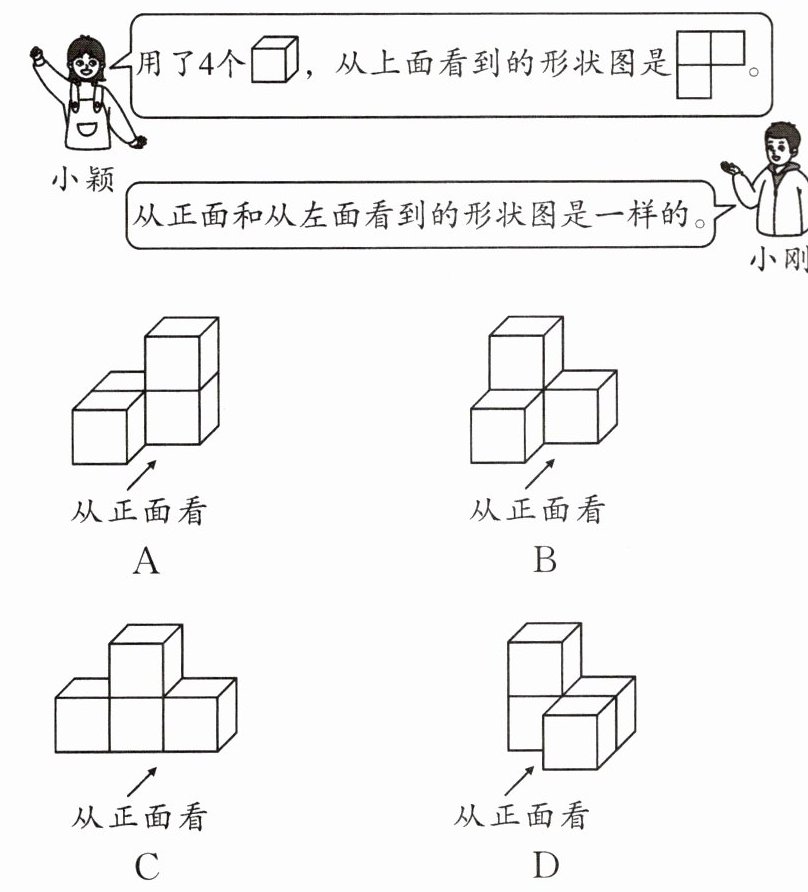
B
)]

答案:
B
10. 如图是由若干个完全相同的小立方块搭成的几何体,若将小立方块①移动到小立方块②的正上方,则下列关于移动后的几何体,从三个不同方向看到的形状图的说法正确的是(
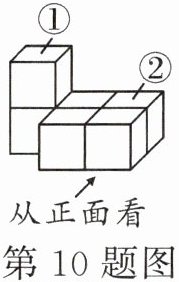
A.从左面看到的形状图发生改变
B.从上面看到的形状图发生改变
C.从正面看到的形状图发生改变
D.从正面、左面、上面看到的形状图都发生改变
C
)
A.从左面看到的形状图发生改变
B.从上面看到的形状图发生改变
C.从正面看到的形状图发生改变
D.从正面、左面、上面看到的形状图都发生改变
答案:
C
11. 如图是由6个大小相同的小立方块搭成的几何体,其中每个小立方块的棱长为1 cm,则这个几何体的表面积(包括底部)为
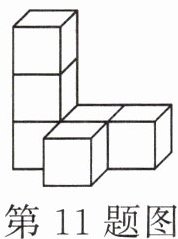
26
$cm^2。$
答案:
26
12. [2023·深圳期中]一个几何体由若干个大小相同的小立方块搭成,如图是从上面看到的这个几何体的形状图,其中正方形中的数字表示在该位置的小立方块的个数。
(1)一共用了__
(2)请在网格中画出从正面和从左面看到的该几何体的形状图;
(3)可以在这个几何体上最多添加__

(1)一共用了__
11
__个小立方块;(2)请在网格中画出从正面和从左面看到的该几何体的形状图;
(3)可以在这个几何体上最多添加__
3
__个大小相同的小立方块,使得从左面和从上面看到的形状图不变。
答案:
1. (1)
计算小立方块的总数:
根据从上面看到的形状图中每个位置的数字,将这些数字相加,即$2 + 3+1 + 1+4=11$(个)。
2. (2)
画从正面看到的形状图:
从正面看,有$3$列,第一列最高有$3$个小立方块,第二列最高有$1$个小立方块,第三列最高有$4$个小立方块。
画从左面看到的形状图:
从左面看,有$3$列,第一列最高有$2$个小立方块,第二列最高有$3$个小立方块,第三列最高有$4$个小立方块(画图略,按照要求画出相应的矩形组合,每列的高度对应相应的数字)。
3. (3)
分析从左面和上面看到的形状图不变的情况:
从左面看,各列的高度分别为$2$,$3$,$4$;从上面看,形状图的分布不变。
对于从上面看到的形状图中数字为$2$的位置,最多可添加$0$个(因为从左面看该列高度为$2$);对于数字为$3$的位置,最多可添加$0$个(从左面看该列高度为$3$);对于数字为$1$的两个位置,从左面看对应的列高度分别为$2$和$3$,第一个$1$的位置(对应左面看第一列)最多可添加$2 - 1=1$个,第二个$1$的位置(对应左面看第二列)最多可添加$3 - 1 = 2$个;对于数字为$4$的位置,最多可添加$0$个(从左面看该列高度为$4$)。
所以最多添加$1+2=3$个。
综上,答案依次为:(1)$11$;(3)$3$。
计算小立方块的总数:
根据从上面看到的形状图中每个位置的数字,将这些数字相加,即$2 + 3+1 + 1+4=11$(个)。
2. (2)
画从正面看到的形状图:
从正面看,有$3$列,第一列最高有$3$个小立方块,第二列最高有$1$个小立方块,第三列最高有$4$个小立方块。
画从左面看到的形状图:
从左面看,有$3$列,第一列最高有$2$个小立方块,第二列最高有$3$个小立方块,第三列最高有$4$个小立方块(画图略,按照要求画出相应的矩形组合,每列的高度对应相应的数字)。
3. (3)
分析从左面和上面看到的形状图不变的情况:
从左面看,各列的高度分别为$2$,$3$,$4$;从上面看,形状图的分布不变。
对于从上面看到的形状图中数字为$2$的位置,最多可添加$0$个(因为从左面看该列高度为$2$);对于数字为$3$的位置,最多可添加$0$个(从左面看该列高度为$3$);对于数字为$1$的两个位置,从左面看对应的列高度分别为$2$和$3$,第一个$1$的位置(对应左面看第一列)最多可添加$2 - 1=1$个,第二个$1$的位置(对应左面看第二列)最多可添加$3 - 1 = 2$个;对于数字为$4$的位置,最多可添加$0$个(从左面看该列高度为$4$)。
所以最多添加$1+2=3$个。
综上,答案依次为:(1)$11$;(3)$3$。
13. [2024·梅州期末]用若干个大小相同的小立方块搭一个几何体,使得从正面和从上面看到的这个几何体的形状图如图所示,则搭成这个几何体至少需要
]
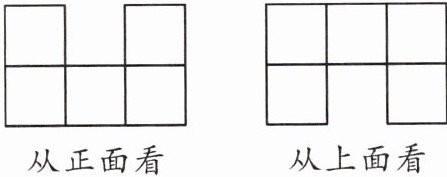
7
个小立方块。]

答案:
7
查看更多完整答案,请扫码查看


