《2025年状元成才路创优作业七年级数学上册北师大版》

7. 有一个方程$\frac{x - ■}{2}= x + 3$,其中“■”表示一个被污渍盖住的常数,答案中此方程的解为$x = - 7$,那么“■”处的常数应是(C)
A.$- 5$
B.$- 1$
C.$1$
D.$5$

答案： C

8. 对于任意有理数$a$,$b$,规定$a※b= \frac{a + 2b}{2}$,则方程$3※(x + 1)= 0.5x - 1$的解是$x=-7$。

答案： $x=-7$

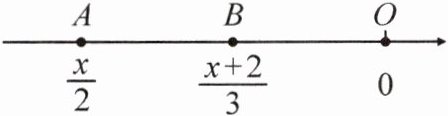
9. 如图,$O$为数轴上的原点,点$A$,$B表示的数分别是\frac{x}{2}$,$\frac{x + 2}{3}$。若$B$,$O两点之间的距离等于A$,$B$两点之间的距离,则$x$的值是-8。
$\begin{array}{c}\begin{array}{|c|c|c|c|}\hline & & & \\\hline & & & \\\hline & & & \\\hline\end{array}\begin{array}{c}\begin{array}{|c|c|c|c|}\hline & & & \\\hline & & & \\\hline & & & \\\hline \end{array}$

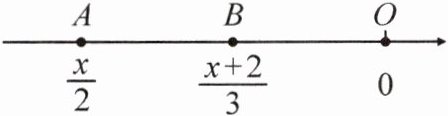
答案： -8

10. 解方程：
(1)$-\frac{1}{2}(x - 2)= 1-\frac{2}{3}(x - 2)$；
(2)$2-\frac{x + 2}{5}= x-\frac{x - 1}{2}$；
(3)$\frac{x + 1}{2}-1= 2+\frac{0.1 - 0.05x}{0.2}$。

答案： 解:
(1)$x=8$。
(2)$x=\frac{11}{7}$。
(3)$x=4$。

11. [教材 P146 习题 T12 变式题]今年弟弟的年龄恰好是哥哥年龄的$\frac{1}{2}$,而 9 年前弟弟的年龄只是哥哥年龄的$\frac{1}{5}$,哥哥今年的年龄是多少？

答案： 解:哥哥今年的年龄为 24 岁。

12. 在解方程$3(x + 1)-\frac{1}{3}(x - 1)= 2(x - 1)-\frac{1}{2}(x + 1)$时,我们可以将$x + 1$,$x - 1$各看成一个整体进行移项、合并同类项,得$\frac{7}{2}(x + 1)= \frac{7}{3}(x - 1)$。再去分母,得$21(x + 1)= 14(x - 1)$,进而解得$x = - 5$。这种方法叫作整体求解法,请用这种方法解方程：
$5(2x + 3)-\frac{3}{4}(x - 2)= 2(x - 2)-\frac{1}{2}(2x + 3)$。

答案： 解:将$2x+3$,$x-2$各看成一个整体进行移项、合并同类项,得$\frac{11}{2}(2x+3)=\frac{11}{4}(x-2)$。去分母,得$22(2x+3)=11(x-2)$,即$2(2x+3)=x-2$。去括号,得$4x+6=x-2$。移项、合并同类项,得$3x=-8$。方程的两边都除以 3,得$x=-\frac{8}{3}$。