第77页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
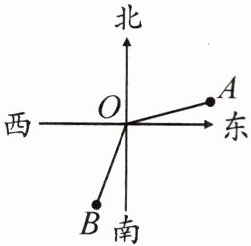
9. 如图,某海域有三个小岛 $ A $,$ B $,$ O $,在小岛 $ O $ 处观测到小岛 $ A $ 在它的北偏东 $ 70^{\circ} $ 方向上,观测到小岛 $ B $ 在它的南偏西 $ 15^{\circ} $ 方向上,则 $ \angle AOB $ 的度数是(
A.$ 85^{\circ} $
B.$ 105^{\circ} $
C.$ 115^{\circ} $
D.$ 125^{\circ} $
D
)
A.$ 85^{\circ} $
B.$ 105^{\circ} $
C.$ 115^{\circ} $
D.$ 125^{\circ} $
答案:
D
10. 比较大小:$ 45^{\circ}45' $______
>
$ 45.45^{\circ} $(填“$>$”“$<$”或“$=$”)。
答案:
>
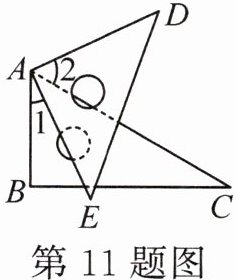
11. 如图,将一个三角尺 $ 60^{\circ} $ 角的顶点与另一个三角尺的直角顶点重合,$ \angle 1 = 25^{\circ}18' $,则 $ \angle 2 = $
55
$^{\circ}$18
$' $。
答案:
55 18
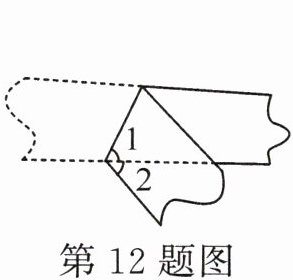
12. 如图,一条纸带的上下两边都是直的,将纸带折叠,若 $ \angle 1 = 65^{\circ} $,则 $ \angle 2 $ 的度数为
50°
。
答案:
50°
13. “双减”政策实施后,某校调查到学生上床休息的时间一般在晚上 $ 9:50 $,该时刻时针与分针的夹角是
5
$^{\circ}$。
答案:
5
14. 已知 $ \angle AOB = 60^{\circ} $,$ \angle AOC = \frac{1}{3}\angle AOB $,射线 $ OD $ 平分 $ \angle BOC $,则 $ \angle COD $ 的度数为
20°或40°
。
答案:
20°或40°
15. 如图,$ OB $,$ OC $ 是 $ \angle AOD $ 内部的两条射线,$ OM $ 平分 $ \angle AOB $,$ ON $ 平分 $ \angle COD $,$ \angle MON = 80^{\circ} $。
(1)若 $ \angle BOC = 40^{\circ} $,求 $ \angle AOD $ 的度数;
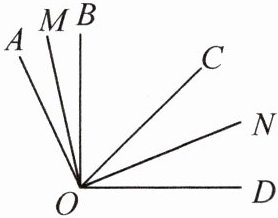
(2)若 $ \angle AOD = x^{\circ} $,求 $ \angle BOC $ 的度数(用含 $ x $ 的代数式表示)。
(1)若 $ \angle BOC = 40^{\circ} $,求 $ \angle AOD $ 的度数;

(2)若 $ \angle AOD = x^{\circ} $,求 $ \angle BOC $ 的度数(用含 $ x $ 的代数式表示)。
答案:
解:
(1)∠AOD=120°。
(2)∠BOC=(160-x)°。
(1)∠AOD=120°。
(2)∠BOC=(160-x)°。
16. 如图,已知锐角 $ \angle \alpha $ 和直角 $ \angle AOB $,在 $ \angle AOB $ 内部求作 $ \angle AOC $,使 $ \angle AOC + \angle \alpha = 90^{\circ} $。
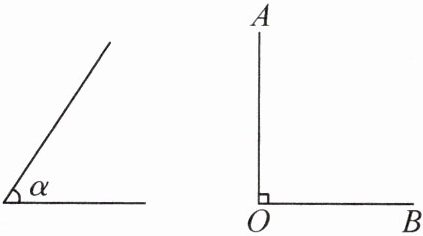

答案:
1. 以∠α的顶点为圆心,任意长为半径画弧,分别交∠α的两边于点M、N;
2. 以点O为圆心,同样长为半径画弧,交OB于点D;
3. 以点D为圆心,MN的长为半径画弧,与步骤2中所画的弧交于点E;
4. 过点O、E作射线OC(OC在∠AOB内部)。
则∠AOC即为所求。
2. 以点O为圆心,同样长为半径画弧,交OB于点D;
3. 以点D为圆心,MN的长为半径画弧,与步骤2中所画的弧交于点E;
4. 过点O、E作射线OC(OC在∠AOB内部)。
则∠AOC即为所求。
17. 过一个多边形的一个顶点的对角线有 $ 6 $ 条,则该多边形是
九
边形,过该多边形的一个顶点的所有对角线可将该多边形分成7
个三角形。
答案:
九 7
18. 如图,甲,乙,丙,丁四个扇形的面积之比为 $ 1:2:4:5 $,则扇形丁的圆心角的度数是
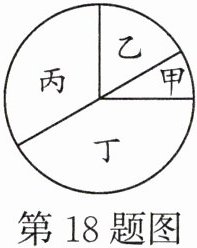
150°
。
答案:
150°
19. 新考向 传统文化·扇面 扇面用于写字作画,是我国古代书法、绘画特有的形式之一,扇面一般都是由两个半径不同的同心圆按照一定的圆心角裁剪而成。如图,一个扇面的圆心角是 $ 120^{\circ} $,大扇形的半径为 $ 20\ cm $,小扇形的半径为 $ 5\ cm $,则这个扇面的面积是
125π cm²
(结果保留 $ \pi $)。
答案:
125π cm²
查看更多完整答案,请扫码查看


