《2025年状元成才路创优作业七年级数学上册北师大版》

1. 计算：$3^{1}= 3$,$3^{2}= 9$,$3^{3}= 27$,$3^{4}= 81$,$3^{5}= 243$,$3^{6}= 729$,…$$。观察运算结果中的规律,猜想 $3^{2025}-1$的个位数字是(C)
A.$8$
B.$6$
C.$2$
D.$0$

答案： C

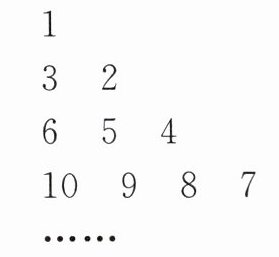
2. 将从 $1$ 开始的连续自然数按如图所示的规律排列,则第 $12$ 行的前两个数的和是155。
```
1
3 2
6 5 4
10 9 8 7
……
```

答案： 155

3. 小王玩撕纸片游戏,如图是一张正方形纸片,他第一次将其撕成四小片,以后每次都将其中一片撕成更小的四片,如此进行下去,当小王撕到第 $n$ 次时,手中共有 $s$ 张纸片。

(1)当小王撕了 $3$ 次时,他手中有几张纸片？
(2)当小王撕了 $n$ 次时,他手中有几张纸片(用含 $n$ 的代数式表示)？

答案： 解:
(1)当小王撕了3次时,他手中有3×3+1=10(张)纸片。
(2)当小王撕了n次时,他手中有(3n+1)张纸片。

4. [教材 $P100$ 问题变式题]试验探究：
如图,在四边形 $ABCD$ 内部,有 $n$ 个点 $P_{i}(i = 1,2,3,…,n)$,连同四边形的 $4$ 个顶点,连接这 $(n + 4)$ 个点,保证所有连线不再相交产生新的点,构造不重叠的小三角形,请把在不同点数情况下最多可构造的小三角形的个数填入表中：

(1)将表中数据补充完整；
(2)当四边形 $ABCD$ 内部有 $2024$ 个点时,求最多可构造的小三角形的个数。

(1)8 10 2n+2
(2)当n=2024时,2n+2=2×2024+2=4050,即最多可构造的小三角形的个数是4050。

答案： 解:
(1)8 10 2n+2
(2)当n=2024时,2n+2=2×2024+2=4050,即最多可构造的小三角形的个数是4050。