第72页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
1. 如图,C,D 是线段 AB 上的两点,若 $ AB = 10\ cm $,$ BC = 4\ cm $,点 D 是线段 AC 的中点,则 AD 的长为(
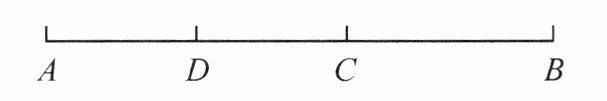
A.$ 2\ cm $
B.$ 3\ cm $
C.$ 4\ cm $
D.$ 6\ cm $
B
)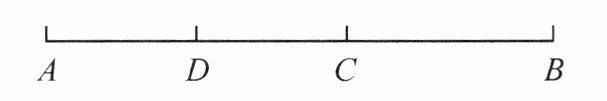
A.$ 2\ cm $
B.$ 3\ cm $
C.$ 4\ cm $
D.$ 6\ cm $
答案:
B
2. 如图,C 为 AB 上一点,$ AC = 30\ cm $,$ BC = \frac{2}{5}AC $,点 D,E 分别为 AC,AB 的中点,则 DE 的长为
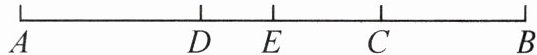
6
$cm$。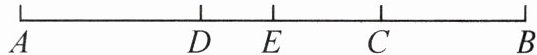
答案:
6
3. 如图,点 B 在线段 AD 上,点 C 是线段 AD 的中点,$ AD = 10 $。
(1)延长线段 AD 到点 E,使 $ DE = BD $(请你依据题意补全图形);
(2)在(1)的条件下,若 $ BC = 4AB $,求线段 AE 的长度。
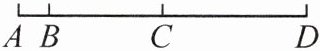
(1)延长线段 AD 到点 E,使 $ DE = BD $(请你依据题意补全图形);
(2)在(1)的条件下,若 $ BC = 4AB $,求线段 AE 的长度。
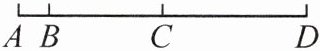
答案:
解:
(1)如图所示。

(2)因为点C是线段AD的中点,AD=10,
所以AC=CD= $\frac{1}{2}$AD=5。
因为BC=4AB,所以AB=1,BC=4,
所以BD=BC+CD=4+5=9,
所以DE=BD=9,所以AE=AD+DE=10+9=19。
解:
(1)如图所示。

(2)因为点C是线段AD的中点,AD=10,
所以AC=CD= $\frac{1}{2}$AD=5。
因为BC=4AB,所以AB=1,BC=4,
所以BD=BC+CD=4+5=9,
所以DE=BD=9,所以AE=AD+DE=10+9=19。
4. 如图,点 C 在线段 AB 的延长线上,$ AB = 12\ cm $,点 M,N 分别是线段 AC,BC 的中点,则 MN 的长度为(
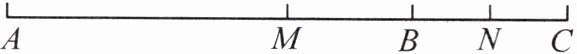
A.$ 24\ cm $
B.$ 12\ cm $
C.$ 8\ cm $
D.$ 6\ cm $
D
)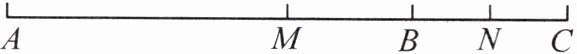
A.$ 24\ cm $
B.$ 12\ cm $
C.$ 8\ cm $
D.$ 6\ cm $
答案:
D
5. 如图,B,C 是线段 AD 上任意两点,点 M 是 AB 的中点,点 N 是 CD 的中点。若 $ MN = 6 $,$ BC = 2 $,求 AD 的长。
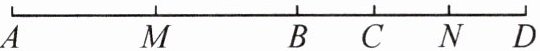
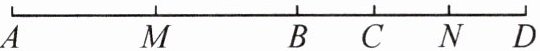
答案:
解:因为点M是AB的中点,所以AB=2BM。
因为点N是CD的中点,所以CD=2CN。
因为MN=BM+BC+CN=6,BC=2,
所以BM+CN=4。
所以AD=AB+BC+CD=2(BM+CN)+BC=2×4+2=10。
因为点N是CD的中点,所以CD=2CN。
因为MN=BM+BC+CN=6,BC=2,
所以BM+CN=4。
所以AD=AB+BC+CD=2(BM+CN)+BC=2×4+2=10。
6. 已知 A,B,C 三点在同一条直线上,且线段 $ AB = 20\ cm $,$ BC = 10\ cm $。若点 M,N 分别为 AB,BC 的中点,则 M,N 两点之间的距离为
15 cm或5 cm
。
答案:
15 cm或5 cm
7. 如图,把一根绳子对折成线段 AB,从点 P 处把绳子剪断,已知 $ AP:BP = 2:3 $,若剪断后的各段绳子中最长的一段为 $ 60\ cm $,求绳子的原长。


答案:
解:因为AP:BP=2:3,所以AP= $\frac{2}{3}$BP。
若这根绳子沿点B对折成线段AB,则剪断后的三段绳子的长度分别为 $\frac{2}{3}$BP, $\frac{2}{3}$BP,2BP,
所以2BP=60 cm,所以BP=30 cm,
则绳子的原长为 $\frac{2}{3}$BP+ $\frac{2}{3}$BP+2BP= $\frac{10}{3}$BP=100 cm;
若这根绳子沿点A对折成线段AB,则剪断后的三段绳子的长度分别为 $\frac{4}{3}$BP,BP,BP,所以 $\frac{4}{3}$BP=60 cm,所以BP=45 cm,
则绳子的原长为 $\frac{4}{3}$BP+BP+BP= $\frac{10}{3}$BP=150 cm。
综上所述,绳子的原长为100 cm或150 cm。
若这根绳子沿点B对折成线段AB,则剪断后的三段绳子的长度分别为 $\frac{2}{3}$BP, $\frac{2}{3}$BP,2BP,
所以2BP=60 cm,所以BP=30 cm,
则绳子的原长为 $\frac{2}{3}$BP+ $\frac{2}{3}$BP+2BP= $\frac{10}{3}$BP=100 cm;
若这根绳子沿点A对折成线段AB,则剪断后的三段绳子的长度分别为 $\frac{4}{3}$BP,BP,BP,所以 $\frac{4}{3}$BP=60 cm,所以BP=45 cm,
则绳子的原长为 $\frac{4}{3}$BP+BP+BP= $\frac{10}{3}$BP=150 cm。
综上所述,绳子的原长为100 cm或150 cm。
查看更多完整答案,请扫码查看


