第59页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
8. 如图所示的运算程序中,若开始输入$x的值是7$,可以得出第$1次输出的结果是12$,第$2次输出的结果是6……$依次继续下去,则第$2024$次输出的结果是(
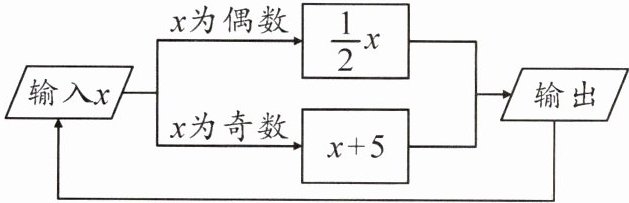
A.$8$
B.$6$
C.$4$
D.$3$
B
)
A.$8$
B.$6$
C.$4$
D.$3$
答案:
B
9. 有若干片相同的拼图,其形状如图①所示(单位:$cm$),凸出的部分是直径为$4cm$的半圆,且拼图沿水平方向排列时可紧密拼成一行,此时底部可与直线贴齐。如图②,当$4$片拼图紧密拼成一行时,长度为$38cm$,则将$n$片拼图紧密拼成一行时,总长度为
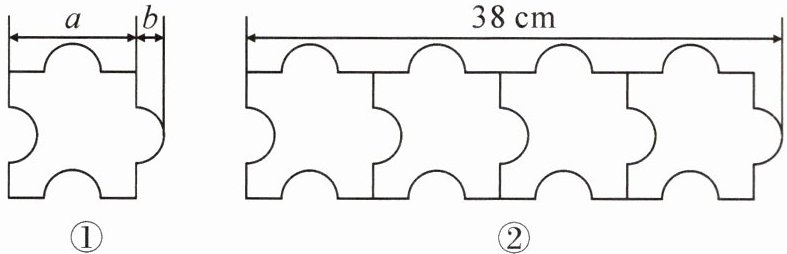
$(9n+2)$
$cm$。
答案:
$(9n+2)$
10. “鱼骨图”是一种发现问题“根本原因”的分析方法,因其形状如鱼骨而得名。如图所示的“鱼骨图”有1条主骨、若干条大骨,每条大骨带有2条中骨。把主骨、大骨、中骨统称为“骨头”。如果这张“鱼骨图”有1条大骨,那么共有4条“骨头”;如果有2条大骨,那么共有7条“骨头”…… (1)如果这张“鱼骨图”有m条大骨,那么共有
(1)如果这张“鱼骨图”有m条大骨,那么共有
 (1)如果这张“鱼骨图”有m条大骨,那么共有
(1)如果这张“鱼骨图”有m条大骨,那么共有(3m+1)
条“骨头”(用含m的代数式表示)。(2)当这张“鱼骨图”有675条大骨时,这张“鱼骨图”共有多少条“骨头”?这张“鱼骨图”共有2026条“骨头”。
(3)如果这张“鱼骨图”有n条中骨,那么共有($\frac {3}{2}n+1$)
条“骨头”(用含n的代数式表示)。
答案:
(1)$(3m+1)$
(2)这张“鱼骨图”共有2026条“骨头”。
(3)$(\frac {3}{2}n+1)$
(1)$(3m+1)$
(2)这张“鱼骨图”共有2026条“骨头”。
(3)$(\frac {3}{2}n+1)$
11. 综合与实践:观察下图,解答下列问题。
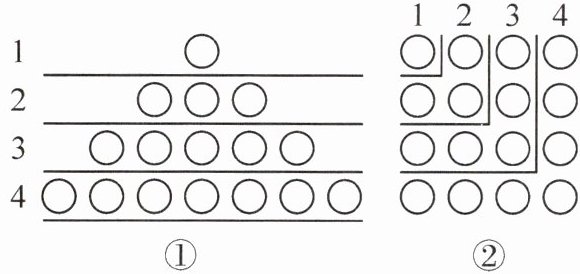
(1)图①的一些圆圈被直线分成$4$层,第$1层有1$个圆圈,第$2层有3$个圆圈,第$3层有5个圆圈……$如果要你继续画下去,那么第$6$层有
(2)对比图①、图②,感受图形的转化,数图中的圆圈个数可以有多种不同的方法。比如:前$2层的圆圈个数和为(1 + 3)或2^{2}$,由此得,$1 + 3 = 2^{2}$。总结规律,从$1开始的n$个连续奇数之和是
(3)运用(2)中的规律计算:$41 + 43 + 45 + … + 199$。

(1)图①的一些圆圈被直线分成$4$层,第$1层有1$个圆圈,第$2层有3$个圆圈,第$3层有5个圆圈……$如果要你继续画下去,那么第$6$层有
11
个圆圈,第$n$层有$(2n-1)$
(用含$n$的代数式表示)个圆圈;(2)对比图①、图②,感受图形的转化,数图中的圆圈个数可以有多种不同的方法。比如:前$2层的圆圈个数和为(1 + 3)或2^{2}$,由此得,$1 + 3 = 2^{2}$。总结规律,从$1开始的n$个连续奇数之和是
$n^{2}$
(用含$n$的代数式表示);(3)运用(2)中的规律计算:$41 + 43 + 45 + … + 199$。
由(2)中的规律可知,原式$=1+3+5+... +199-(1+3+5+... +39)=100^{2}-20^{2}=10000-400=9600$。
答案:
(1)11 $(2n-1)$
(2)$n^{2}$
(3)由
(2)中的规律可知,原式$=1+3+5+... +199-(1+3+5+... +39)=100^{2}-20^{2}=10000-400=9600$。
(1)11 $(2n-1)$
(2)$n^{2}$
(3)由
(2)中的规律可知,原式$=1+3+5+... +199-(1+3+5+... +39)=100^{2}-20^{2}=10000-400=9600$。
查看更多完整答案,请扫码查看


