《2025年状元成才路创优作业七年级数学上册北师大版》

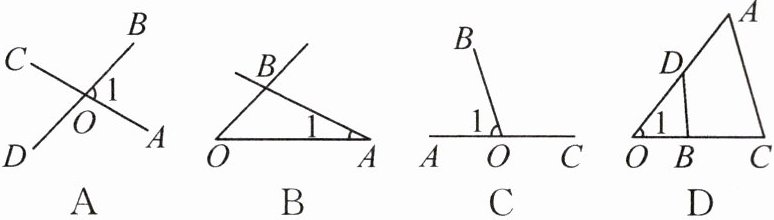
12. [2024·焦作期末]下列四个图中,能用$\angle 1$,$\angle AOB$,$\angle O$三种方法表示同一个角的图形是(D)

答案： D

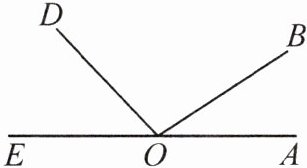
13. 如图,$O$ 是直线 $AE$ 上一点,则图中小于平角的角有5个。

答案： 5

14. 计算：
(1)$32^{\circ}17'53'' + 42^{\circ}42'7''= $75$^{\circ}$；
(2)$90^{\circ} - 78^{\circ}19'40''= $11$^{\circ}$______40$' $______20$''$。

答案：
(1)75
(2)11 40 20

15. 数学课上,小睿同学看了一眼教室墙上挂的钟表,发现时间是 $10:30$,他马上用所学的数学知识计算出了此时时针与分针的夹角的度数,这个度数是135°。

答案： 135°

16. 如图,一幅地图上有 $A$,$B$,$C$ 三地,地图被墨迹污染,导致 $C$ 地具体位置看不清楚了,但知道 $C$ 地在 $A$ 地的北偏东 $30^{\circ}$方向,在 $B$ 地的东南方向。请你确定 $C$ 地的位置。

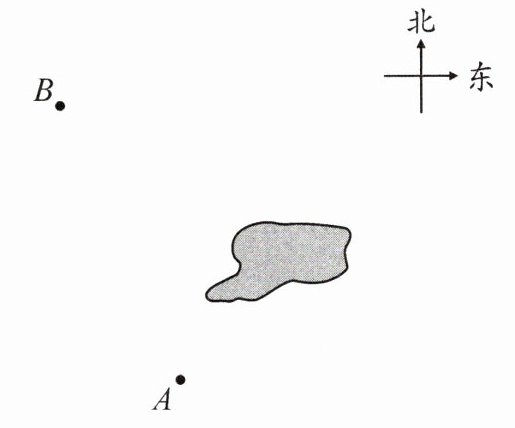
答案：
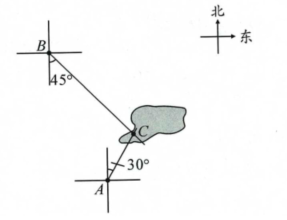
如图所示：

17. 新考向 规律探索
(1)如图①,在$\angle AOB$内部画 1 条射线 $OC$,则图中有3个不同的角；
(2)如图②,在$\angle AOB$内部画 2 条射线 $OC$,$OD$,则图中有6个不同的角；
(3)如图③,在$\angle AOB$内部画 3 条射线 $OC$,$OD$,$OE$,则图中有10个不同的角；
(4)在$\angle AOB$内部画 10 条射线 $OC$,$OD$,$OE$,…,则图中有66个不同的角；
(5)在$\angle AOB$内部画 $n$ 条射线 $OC$,$OD$,$OE$,…,则图中有多少个不同的角？
在∠AOB内部画n条射线OC，OD，OE，…，则图中有1+2+3+…+n+(n+1)=$\frac{(n+1)(n+2)}{2}$(个)不同的角。

答案： 解:
(1)3
(2)6
(3)10
(4)66
(5)在∠AOB内部画n条射线OC，OD，OE，…，则图中有1+2+3+…+n+(n+1)=$\frac{(n+1)(n+2)}{2}$(个)不同的角。