《2025年状元成才路创优作业七年级数学上册北师大版》

1. 下列图形中是多边形的是 (D)

答案： D

2. 从七边形的一个顶点出发,最多可以引出该七边形的对角线的条数是 (D)
A.7
B.6
C.5
D.4

答案： D

3. [教材 P131 习题 T3 变式题]如果从多边形的一个顶点出发作它的对角线,能将多边形分成 10 个三角形,那么这个多边形是十二边形。

答案： 十二

4. 新考向 情境题·蜂巢 蜜蜂是世界上最神奇的昆虫之一,其建造的蜂巢结构稳固,它由一个个紧密排列的“房间”组成(如图),“房间”的横截面是正六边形。若一个正六边形的一边长为 4 mm,则这个正六边形的周长为24mm。

答案： 24

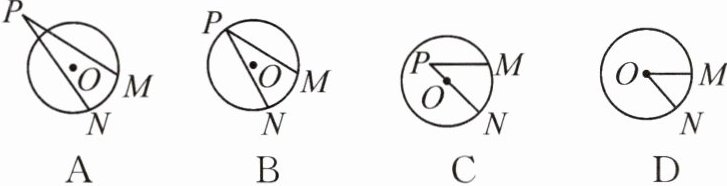
5. 下面四个图中的角为圆心角的是 (D)

答案： D

6. [教材 P130 随堂练习 T2 变式题]将一个圆分成三个扇形甲、乙、丙,其中甲、乙所占总面积的百分比如图所示,那么扇形丙的圆心角的度数是(B)

A.$30^{\circ}$
B.$108^{\circ}$
C.$110^{\circ}$
D.$120^{\circ}$

答案： B

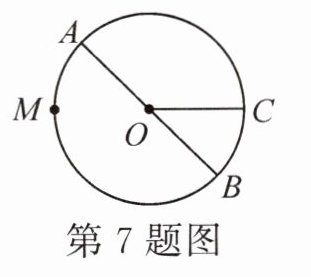
7. 如图所示的圆可记作圆 $O$,可以用字母表示的半径有3条,分别是OA,OB,OC,请写出任意三条弧：$\overset{\frown}{AC}$,$\overset{\frown}{BC}$,$\overset{\frown}{MB}$(答案不唯一)。

答案： 3 OA,OB,OC $\overset{\frown}{AC}$,$\overset{\frown}{BC}$,$\overset{\frown}{MB}$(答案不唯一)

8. 扇形的半径为 6,圆心角的度数为 $60^{\circ}$,则该扇形的面积为6π(结果保留 $\pi$)。

答案： 6π

9. 将一个圆分割成三个扇形,它们的面积之比为 $3 : 4 : 5$,则最小扇形的圆心角的度数为 (A)
A.$90^{\circ}$
B.$120^{\circ}$
C.$180^{\circ}$
D.$270^{\circ}$

答案： A

10. 把一个四边形锯掉一个角,剩下的多边形不可能是 (D)
A.三角形
B.四边形
C.五边形
D.六边形
变式题 [逆向变式]一个多边形截去一个角后,变成一个六边形,则这个多边形原来的边数是______。

答案： D [变式题] 5或6或7

11. 新考向 类比探究 (1)【特例】观察图形并填空：
一个四边形有2条对角线；
一个五边形有5条对角线；
一个六边形有9条对角线。
(2)【探究】由 $n(n ＞ 3)$ 边形的一个顶点出发,可作(n-3)条对角线；$n$ 边形有 $n$ 个顶点,若允许重复计数,则共可作n(n-3)条对角线。
(3)【结论】一个 $n$ 边形有$\frac{n(n-3)}{2}$条对角线。
(4)【应用】一个十二边形有54条对角线。

答案：
(1)2 5 9
(2)(n-3) n(n-3)
(3)$\frac{n(n-3)}{2}$
(4)54