第25页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
1 [中]如图,在数轴上,点 $ A $ 表示数 $ a $,点 $ B $ 表示数 $ b $,点 $ C $ 表示数 $ c $,$ b $ 是最小的正整数,且 $ a $,$ c $ 满足 $ |a + 2| + (c - 6)^2 = 0 $。

(1) $ a = $
(2) 若将数轴折叠,使得点 $ A $ 与点 $ C $ 重合,则折痕与数轴的交点所表示的数为

(1) $ a = $
-2
,$ b = $1
,$ c = $6
。(2) 若将数轴折叠,使得点 $ A $ 与点 $ C $ 重合,则折痕与数轴的交点所表示的数为
2
,点 $ B $ 与数3
对应的点重合,这时若 $ M $,$ N $($ M $ 在 $ N $ 的左侧)两点之间的距离为 $ 2022 $,且 $ M $,$ N $ 两点经折叠后重合,则点 $ M $ 表示的数是-1009
,点 $ N $ 表示的数是1013
。
答案:
(1)-2 1 6
(2)2 3 -1009 1013
(1)-2 1 6
(2)2 3 -1009 1013
2 [2024 江西上饶期末,中]在一条可以折叠的数轴上,点 $ A $,$ B $ 表示的数分别是 $ -10 $,$ 3 $,如图,以点 $ C $ 为折点,将此数轴向右对折,若折叠后的点 $ A $ 在点 $ B $ 的右边,且 $ A $,$ B $ 间距离为 $ 1 $,则点 $ C $ 表示的数是(

A.$ -2 $
B.$ 2 $
C.$ -3 $
D.$ 3 $
C
)
A.$ -2 $
B.$ 2 $
C.$ -3 $
D.$ 3 $
答案:
C
3 [2024 黑龙江哈尔滨调研,中]如图,折叠纸面上一数轴,使得表示数 $ 5 $ 与数 $ -1 $ 的两点重合,若此时,数轴上的 $ A $,$ B $ 两点也重合,且 $ A $,$ B $ 两点之间的距离为 $ 32 $,则点 $ A $ 表示的数为
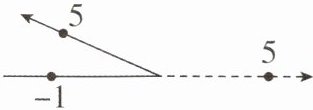
18或-14
。
答案:
18或-14
4 [2024 浙江金华期中,中]在数轴上剪下 $ 8 $ 个单位长度(从 $ 1 $ 到 $ 9 $)的一条线段,并把这条线段沿某点折叠,然后在重叠部分某处剪一刀得到三条线段(如图)。若这三条线段的长度之比为 $ 1:1:2 $,则折痕与数轴的交点所表示的数可能是

4或5或6
。
答案:
4或5或6
5 [2024 广东佛山期末,中]正六边形 $ ABCDEF $ 在数轴上的位置如图,点 $ A $,$ F $ 对应的数分别为 $ 0 $和 $ 1 $,若正六边形(六条边相等)$ ABCDEF $ 绕着顶点按顺时针方向在数轴上连续翻转,翻转 $ 1 $次后,点 $ E $ 所对应的数为 $ 2 $,则连续翻转 $ 2021 $次后,数轴上 $ 2021 $ 这个数所对应的点是(
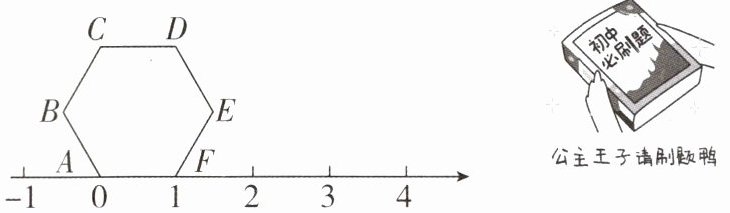
A.$ A $ 点
B.$ B $ 点
C.$ C $ 点
D.$ D $ 点
B
)
A.$ A $ 点
B.$ B $ 点
C.$ C $ 点
D.$ D $ 点
答案:
B
6 [2024 福建泉州期中,中]已知 $ A $,$ B $ 在数轴上对应的数分别用 $ a $,$ b $ 表示,且 $ (ab + 150)^2 + |b + 10| = 0 $,$ P $ 是数轴上的一个动点。动点 $ P $ 从原点开始第一次向右移动 $ 1 $ 个单位长度,第二次向左移动 $ 3 $ 个单位长度,第三次向右移动 $ 5 $ 个单位长度,第四次向左移动 $ 7 $ 个单位长度,…,点 $ P $ 在移动过程中,第
15
次移动所得的对应点与点 $ A $ 重合。
答案:
15
7 [2024 山东日照质检,中]如图,在纸面所在的平面内,一只电子蚂蚁从数轴上表示原点的位置 $ O $ 点出发,按向上、向右、向下、向右的方向依次不断移动,每次移动 $ 1 $ 个单位长度,其移动路线如图所示,第 $ 1 $ 次移动到 $ A_1 $,第 $ 2 $ 次移动到 $ A_2 $,第 $ 3 $ 次移动到 $ A_3 $,…,第 $ n $ 次移动到 $ A_n $,则三角形 $ OA_2A_{2020} $ 的面积是(
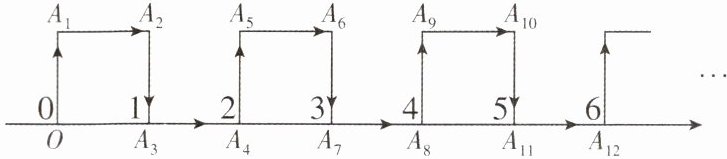
A.$ \dfrac{1009}{2} $
B.$ 505 $
C.$ \dfrac{1011}{2} $
D.$ 506 $
B
)
A.$ \dfrac{1009}{2} $
B.$ 505 $
C.$ \dfrac{1011}{2} $
D.$ 506 $
答案:
B
查看更多完整答案,请扫码查看


