第21页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
1 [2025天津河西区期中]关于$(-5)^{3}$,下列说法不正确的是(
A.表示$(-5)× (-5)× (-5)$
B.底数是$-5$,指数是$3$
C.读作$-5的3$次方
D.计算结果等于$125$
D
)A.表示$(-5)× (-5)× (-5)$
B.底数是$-5$,指数是$3$
C.读作$-5的3$次方
D.计算结果等于$125$
答案:
D 【解析】$(-5)^3=-125$,故选 D.
2 [2024湖南永州期末]下列说法正确的是(
A.$-2^{8}的底数是-2$
B.$2^{5}表示5个2$相加
C.$(-3)^{3}与-3^{3}$意义相同
D.$-\left(\dfrac {2}{3}\right)^{3}的底数是\dfrac {2}{3}$
D
)A.$-2^{8}的底数是-2$
B.$2^{5}表示5个2$相加
C.$(-3)^{3}与-3^{3}$意义相同
D.$-\left(\dfrac {2}{3}\right)^{3}的底数是\dfrac {2}{3}$
答案:
D 【解析】A 选项,$-2^8$的底数是 2,此选项的说法错误,故不符合题意;B 选项,$2^5$表示 5个2相乘,此选项的说法错误,故不符合题意;C 选项,$(-3)^3$表示3个-3相乘,$-3^3$表示3个3相乘的相反数,它们表示的意义不同,此选项的说法错误,故不符合题意;D 选项,$-\left(\frac{2}{3}\right)^3$的底数是$\frac{2}{3}$,此选项的说法正确,故此选项符合题意.故选 D.
3 [2025云南昆明期中]$-4^{2}$等于(
A.$-8$
B.$8$
C.$-16$
D.$16$
C
)A.$-8$
B.$8$
C.$-16$
D.$16$
答案:
C 【解析】$-4^2=-4×4=-16$,故选 C.
4 [2025湖南衡阳期中]数$a的平方等于36$,那么数$a$可能是(
A.$6$
B.$-6$
C.$\pm 6$
D.$\pm 18$
C
)A.$6$
B.$-6$
C.$\pm 6$
D.$\pm 18$
答案:
C 【解析】因为$(\pm 6)^2=36$,所以$a=\pm 6$,故选 C.
5 [2025湖南衡阳质检]$(-1)^{2024}$的相反数是
-1
。
答案:
-1 【解析】$(-1)^{2024}=1$,1 的相反数是-1,故答案为-1.
6 [2025湖北武汉期中]若$x^{2}= 9$,$\vert y\vert =4$,且$xy<0$,则$x + y= $
±1
。
答案:
±1 【解析】因为$x^2=9$,$|y|=4$,$(\pm 3)^2=9$,所以$x=\pm 3$,$y=\pm 4$.因为$xy<0$,所以$x=3$,$y=-4$或$x=-3$,$y=4$.当$x=3$,$y=-4$时,$x+y=3-4=-1$;当$x=-3$,$y=4$时,$x+y=-3+4=1$.综上,$x+y=\pm 1$.故答案为$\pm 1$.
7 计算:
(1)$-(-2)^{4}$; (2)$-2^{3}+(-3)^{2}$;
(3)$\left(-1\dfrac {1}{3}\right)^{2}× (-0.5)^{3}$;
(4)$-1^{3}-3× (-1)^{3}$.
(1)$-(-2)^{4}$; (2)$-2^{3}+(-3)^{2}$;
(3)$\left(-1\dfrac {1}{3}\right)^{2}× (-0.5)^{3}$;
(4)$-1^{3}-3× (-1)^{3}$.
答案:
【解】
(1)原式=-16.
(2)原式=-8+9=1.
(3)原式=$\frac{16}{9}×\left(-\frac{1}{8}\right)=-\frac{2}{9}$.
(4)原式=-1+3=2.
(1)原式=-16.
(2)原式=-8+9=1.
(3)原式=$\frac{16}{9}×\left(-\frac{1}{8}\right)=-\frac{2}{9}$.
(4)原式=-1+3=2.
8 [2024湖南怀化期末]一张纸的厚度大约为$0.09\mathrm{mm}$,如图,将其对折、压平,称作第$1$次操作;再将其对折、压平,称作第$2$次操作;…$$.假设这张纸足够大,每一次也能压得足够平整,如此重复,则第$10$次操作后的厚度最接近于(
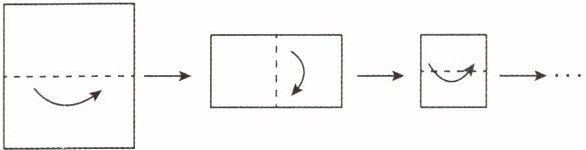
A.数学课本的厚度
B.姚明的身高
C.一层楼房的高度
D.一支中性笔的长度
D
)
A.数学课本的厚度
B.姚明的身高
C.一层楼房的高度
D.一支中性笔的长度
答案:
D 【解析】由题知,第1次操作后的厚度为$(0.09×2)\ mm$;第2次操作后的厚度为$(0.09×2^2)\ mm$;第3次操作后的厚度为$(0.09×2^3)\ mm$;…,所以第10次操作后的厚度为$0.09×2^{10}=0.09×1024=92.16\ (mm)$,所以第10次操作后的厚度最接近于一支中性笔的长度.故选 D.
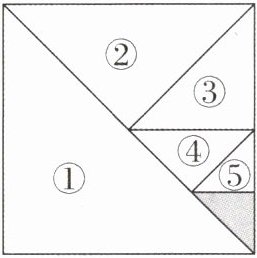
9 [2025山东泰安期中,较难]数形结合是解决数学问题的一种重要思想方法.如图所示,将一个边长为$1的正方形纸片分成6$个部分,部分①的面积是边长为$1$的正方形纸片面积的一半,部分②的面积是部分①面积的一半,部分③的面积是部分②面积的一半,…,以此类推.
(1)阴影部分的面积是______.
(2)受(1)的启发,试求出$\dfrac {1}{2}+\dfrac {1}{2^{2}}+\dfrac {1}{2^{3}}+\dfrac {1}{2^{4}}+\dfrac {1}{2^{5}}$的值.
(3)计算:$\dfrac {1}{2}+\dfrac {1}{2^{2}}+\dfrac {1}{2^{3}}+… +\dfrac {1}{2^{100}}= $______.
(1)
(2)
(3)
(1)阴影部分的面积是______.
(2)受(1)的启发,试求出$\dfrac {1}{2}+\dfrac {1}{2^{2}}+\dfrac {1}{2^{3}}+\dfrac {1}{2^{4}}+\dfrac {1}{2^{5}}$的值.
(3)计算:$\dfrac {1}{2}+\dfrac {1}{2^{2}}+\dfrac {1}{2^{3}}+… +\dfrac {1}{2^{100}}= $______.

(1)
$\frac{1}{32}$
(2)
根据题意可得$\frac{1}{2}+\frac{1}{2^2}+\frac{1}{2^3}+\frac{1}{2^4}+\frac{1}{2^5}=1-\frac{1}{32}=\frac{31}{32}$
(3)
$1-\frac{1}{2^{100}}$
答案:
【解】
(1)根据题意可得,阴影部分的面积占边长为1的正方形纸片面积的$\frac{1}{2}×\frac{1}{2}×\frac{1}{2}×\frac{1}{2}×\frac{1}{2}=\left(\frac{1}{2}\right)^5=\frac{1}{32}$,所以阴影部分的面积是$1×\frac{1}{32}=\frac{1}{32}$,故答案为$\frac{1}{32}$.
(2)根据题意可得$\frac{1}{2}+\frac{1}{2^2}+\frac{1}{2^3}+\frac{1}{2^4}+\frac{1}{2^5}=1-\frac{1}{32}=\frac{31}{32}$.
(3)$\frac{1}{2}+\frac{1}{2^2}+\frac{1}{2^3}+\cdots+\frac{1}{2^{100}}=1-\frac{1}{2^{100}}$,故答案为$1-\frac{1}{2^{100}}$.
(1)根据题意可得,阴影部分的面积占边长为1的正方形纸片面积的$\frac{1}{2}×\frac{1}{2}×\frac{1}{2}×\frac{1}{2}×\frac{1}{2}=\left(\frac{1}{2}\right)^5=\frac{1}{32}$,所以阴影部分的面积是$1×\frac{1}{32}=\frac{1}{32}$,故答案为$\frac{1}{32}$.
(2)根据题意可得$\frac{1}{2}+\frac{1}{2^2}+\frac{1}{2^3}+\frac{1}{2^4}+\frac{1}{2^5}=1-\frac{1}{32}=\frac{31}{32}$.
(3)$\frac{1}{2}+\frac{1}{2^2}+\frac{1}{2^3}+\cdots+\frac{1}{2^{100}}=1-\frac{1}{2^{100}}$,故答案为$1-\frac{1}{2^{100}}$.
查看更多完整答案,请扫码查看


