《2025年初中必刷题七年级数学上册湘教版》

1 [2025 江苏南京质检,中]已知下列方格中的 E、F、G、H、I 这五个字母各表示一个数,且任意 3 个连续方格中的数之和为 10,则 $E+F+G+H+I$的值为(B)
A.19
B.26
C.37
D.39

答案： B 【解析】用x表示E和3之间的方格里的数. 因为任意3个连续方格中的数之和为10，所以E+x+3=x+3+F=3+F+G=F+G+H=G+H+I=H+I+(-1)=10，所以易知E=F，H=3，F=I，所以I=10-3-(-1)=10-3+1=8，所以E=F=8，G+3+8=10，所以G=-1，所以E+F+G+H+I=8+8+(-1)+3+8=26. 故选 B.

2 [2025 内蒙古通辽期中,中]我们定义一种新运算,规定:表示 $a - b + c$,表示 $-x + y - z$,则+\的值为______.

答案：
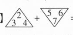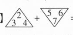-3 【解析】=2-3+4+(-5+6-7)=2-3+4-5+6-7=-3，故答案为-3.

3 [2025 湖南衡阳期中,中]若 $|a| = 2$, $|b| = 3$, $|c| = 6$, $|a + b| = -(a + b)$, $|b + c| = b + c$,计算 $a + b - c$的值.

答案： 【解】因为|a|=2，|b|=3，|c|=6，所以a=±2，b=±3，c=±6. 因为|a+b|=-(a+b)，|b+c|=b+c，所以a+b≤0，b+c≥0，所以a=±2，b=-3，c=6，所以当a=2，b=-3，c=6时，a+b-c=2+(-3)-6=-7；当a=-2，b=-3，c=6时，a+b-c=-2+(-3)-6=-11. 综上，a+b-c的值为-7或-11.

4 [中](1)在 8 个连续整数 $1,2,3, …,8$ 的前面,恰当地添上正号或者负号,使它们的和为 0. 请写出两种不同的算式.
(2)在 $n$ 个连续整数 $1,2,3, …,n$ 的前面,恰当地添上正号或者负号,使它们的和的绝对值最小,求这个最小值.

答案： 【解】
(1)1-2+3-4-5+6-7+8=0或-1+2-3+4+5-6+7-8=0.(答案不唯一)
(2)①当n=4k(k为正整数)时，可以添加正号或者负号让每4个连续整数的和为0，这时它们和的绝对值最小，为0.
②当n=4k+1(k为正整数)时，可以保留整数1，在余下的4k个整数前面添加正号或者负号使其和为0，这时它们和的绝对值最小，为1.
③当n=4k+2(k为正整数)时，可以保留整数1,2，在余下的4k个整数前面添加正号或者负号使其和为0. 令-1+2=1或1-2=-1，则这时它们和的绝对值最小，为1.
④当n=4k+3(k为正整数)时，可以保留整数1,2,3，在余下的4k个整数前面添加正号或者负号使其和为0. 令1+2-3=0或-1-2+3=0，则这时它们和的绝对值最小，为0.

5 [较难]国庆期间,某特技飞行队在黄山湖公园进行特技表演,其中一架飞机起飞后的高度变化如下表所示.
(1)经过 4 次变化后这架飞机比起飞点高了多少千米?
(2)如果飞机每上升或下降 1 km 需消耗 2 升燃油,那么这架飞机在这 4 个动作表演过程中,一共消耗了多少升燃油?
(3)如果飞机进行特技表演时,有 4 个规定动作,起飞后高度变化如下:上升 3.8 km,下降 2.9 km,再上升 1.6 km,若要使飞机最终比起飞点高出 1 km,问第 4 个动作是上升还是下降,需上升或下降多少千米?

答案： 【解】
(1)4.4+(-3.2)+(+1.1)+(-1.5)=0.8(km).
答：这架飞机比起飞点高了0.8 km.
(2)(4.4+3.2+1.1+1.5)×2=20.4(升).
答：这架飞机在这4个动作表演过程中，一共消耗了20.4升燃油.
(3)1-(3.8-2.9+1.6)=-1.5(km).
答：第4个动作是下降，需下降1.5 km.

6 核心素养运算能力 [难][尝试]
(1)比较大小(用“＞”“＜”或“=”填空):
①$|-2| + |3|$＞$|-2 + 3|$;
②$|-6| + |4|$＞$|-6 + 4|$;
③$|-3| + |-4|$=$|-3 - 4|$;
④$|0| + |-7|$=$|0 - 7|$.
[归纳]
(2)观察上面的数量关系,可以得到:$|a| + |b|$≥$|a + b|$(用“＞”“＜”“=”“≥”或“≤”填空).
[应用]
(3)利用上面得到的结论解决下面问题:
若$|m| + |n| = 16$, $|m + n| = 2$,则 $m = $±9或±7.

答案： 【解】
(1)①因为|-2|+|3|=2+3=5，|-2+3|=1，所以|-2|+|3|＞|-2+3|；
②因为|-6|+|4|=6+4=10，|-6+4|=2，所以|-6|+|4|＞|-6+4|；
③因为|-3|+|-4|=3+4=7，|-3-4|=7，所以|-3|+|-4|=|-3-4|；
④因为|0|+|-7|=0+7=7，|0-7|=7，所以|0|+|-7|=|0-7|. 故答案为＞,＞,=,=.
(2)观察
(1)的结论可得，|a|+|b|≥|a+b|.故答案为≥.
(3)因为|m|+|n|=16，|m+n|=2，所以m，n异号.
①当m为正数，n为负数时，|m|+|n|=m-n=16，即n=m-16. 将n=m-16代入|m+n|=2，得|m+m-16|=2，解得m=9或m=7，符合题设；
②当m为负数，n为正数时，|m|+|n|=-m+n=16，即n=m+16. 将n=m+16代入|m+n|=2，得|m+m+16|=2，解得m=-9或m=-7，符合题设.
综上，m=±9或m=±7. 故答案为±9或±7.