《2025年初中必刷题七年级数学上册湘教版》

9 [2025 安徽合肥期中,中]根据图中情景,解答下列问题：

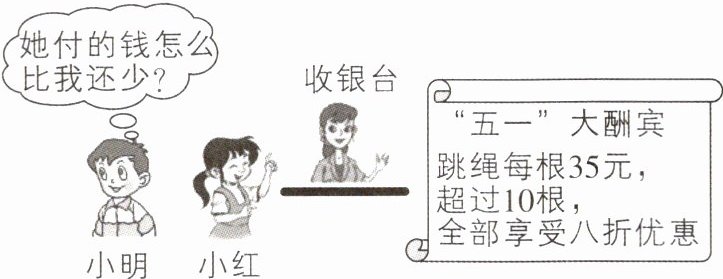
(1)购买 8 根跳绳需280元；购买 12 根跳绳需______336元.
(2)购买 $ m $ 根跳绳需多少元？(请用含有 $ m $ 的式子表示)
(3)小红比小明多买 2 根,付款时小红反而比小明少 7 元,你认为这种情况有可能吗？请利用方程知识说明理由.

答案： 【解】
(1)根据题意得$35×8=280$(元),即购买8 根跳绳需 280 元.$0.8×35×12=336$(元),即购买 12 根跳绳需 336 元. 故答案为 280,336.
(2)当$m≤10$时,需 35m 元;当$m＞10$时,需$35m×0.8=28m$(元).
(3)这种情况有可能. 理由如下:若小红比小明多买2根,付款时小红反而比小明少7元成立,则唯一的可能性就是小红买的跳绳超过10 根,全部享受八折优惠,而小明买的跳绳不足 10 根,没享受优惠,设小明买了 x 根跳绳,则小红买了$(x+2)$根跳绳. 根据题意得$35x-35×0.8(x+2)=7$,解得$x=9,x+2=11＞10$(符合题意).故这种情况有可能,即小明买了9根跳绳,小红买了 11 根跳绳.

10 [2024 湖北荆门期中,较难]观察下列三行数,回答下面的问题：
$ -2,4,-8,16,-32,… $；①
$ 0,6,-6,18,-30,… $；②
$ 3,-3,9,-15,33,… $. ③
(1)第①行数的第 7 个数是-128.
(2)设第①行数的第 $ n $ 个数为 $ a $,写出第②行数的第 $ n $ 个数是a+2(用含 $ a $ 的式子表示).
(3)取每行数中的第 $ m $ 个数,则第①②③行这三个数的和能否等于 - 509？如果能,请你求出 $ m $ 的值；如果不能,请说明理由.
能. 根据题意,可得第③行数的第n个数等于第①行数的第n个数的相反数加上 1.设第①②③行中的第 m 个数分别为 x,$x+2,$$-x+1$. 由题意得$x+x+2+(-x+1)=-509$,解得$x=-512.$因为$(-1)^{9}×2^{9}=-512$,所以$m=9.$

答案： 【解】
(1)根据题意,可知第①行数的第n个数为$(-1)^{n}×2^{n}$,所以第①行数的第7个数是$(-1)^{7}×2^{7}=-128$. 故答案为-128.
(2)根据题意,可得第②行数的第n个数等于第①行数的第n个数加上 2.因为第①行数的第n个数为a,所以第②行数的第n个数是$a+2$. 故答案为$a+2.$
(3)能. 根据题意,可得第③行数的第n个数等于第①行数的第n个数的相反数加上 1.设第①②③行中的第 m 个数分别为 x,$x+2,$$-x+1$. 由题意得$x+x+2+(-x+1)=-509$,解得$x=-512.$因为$(-1)^{9}×2^{9}=-512$,所以$m=9.$

11 [2024 云南楚雄期末,较难]甲、乙两工程队想共同承包一项工程,甲队单独做这项工程需 30 天完成,乙队单独做这项工程需 20 天完成,合同规定 15 天完成,否则每超过一天罚款 1 000 元,甲、乙两队经商量后签订了该合同.
(1)正常情况下,甲、乙两队能否履行该合同？为什么？
(2)现两队合作完成这项工程的 75%,因别处有急事,必须调走一个队,问调走哪个队更合适？为什么？

答案： 【解】
(1)正常情况下,甲、乙两队能履行该合同. 理由如下:设甲、乙两队合作需x天完成这项工程. 根据题意得$\frac {x}{30}+\frac {x}{20}=1$,解得$x=12$. 因为$12＜15$,所以正常情况下,甲、乙两队能履行该合同.
(2)调走甲队更合适. 理由如下:设调走乙队,甲队还需 m 天完成这项工程. 根据题意得$\frac {m}{30}+75\% =1$,解得$m=\frac {15}{2}$,所以$12×75\% +\frac {15}{2}=\frac {33}{2}$(天). 因为$\frac {33}{2}＞15$,所以调走乙队不合适. 设调走甲队,乙队还需n天完成这项工程. 根据题意得$\frac {n}{20}+75\% =1$,解得$n=5$,所以$12×75\% +5=14$(天). 因为$14＜15$,所以调走甲队合适.

12 [2025 湖南岳阳质检,中]数轴上,两点之间的距离可以用这两点中右边的点所表示的数减去左边的点所表示的数来计算,例如：数轴上 $ M,N $ 两点表示的数分别是 - 1 和 2,那么 $ M,N $ 两点之间的距离就是 $ MN = 2 - (-1) = 3 $. 如图,在数轴上点 $ A $ 表示的数是 4,点 $ B $ 位于点 $ A $ 的左侧,与点 $ A $ 的距离是 10 个单位长度.
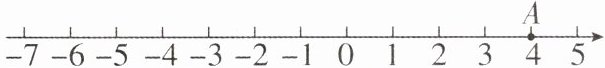
(1)点 $ B $ 表示的数是-6,并在数轴上将点 $ B $ 表示出来.
(2)动点 $ P $ 从点 $ B $ 出发,沿着数轴的正方向,以每秒 2 个单位长度的速度运动,求经过多少秒,点 $ P $ 与点 $ A $ 的距离是 2 个单位长度.
(3)在(2)的条件下,点 $ P $ 出发的同时,点 $ Q $ 从点 $ A $ 出发,沿着数轴的负方向,以每秒 4 个单位长度的速度运动. 若点 $ Q $ 运动到点 $ B $ 的左侧,且点 $ Q $ 与点 $ B $ 的距离是 6 个单位长度,求此时点 $ P $ 与点 $ Q $ 的距离.

答案： 【解】
(1)因为在数轴上点 A 表示的数是 4,点 B 位于点 A 的左侧,与点 A 的距离是 10个单位长度,所以点 B 表示的数是$4-10=-6$,故答案为-6. 在数轴上表示点 B 如图所示.![img alt=数轴]
(2)设经过t秒,点 P 与点 A 的距离是2个单位长度.因为动点 P 从点 B 出发,沿着数轴的正方向,以每秒2个单位长度的速度运动,所以经过t秒,点 P 所表示的数为$-6+2t$. 当点 P 在点 A 左侧时,可得$4-(-6+2t)=2$,解得$t=4$;当点 P 在点 A 右侧时,可得$(-6+2t)-4=2$,解得$t=6.$综上所述,经过4秒或6秒,点 P 与点 A 的距离是2个单位长度.
(3)设经过a秒,点 Q 运动到点 B 的左侧,且点 Q 与点 B 的距离是6个单位长度. 因为在
(2)的条件下,点 P 出发的同时,点 Q 从点 A 出发,沿着数轴的负方向,以每秒4个单位长度的速度运动,所以经过a秒,点 P 所表示的数为$-6+2a$,点 Q 所表示的数为$4-4a.$根据题意可得$-6-(4-4a)=6$,解得$a=4,$则点 P 所表示的数为$-6+2×4=2$,点 Q 所表示的数为$4-4×4=-12,$所以点 P 与点 Q 的距离是$2-(-12)=14.$