第69页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
1 [2025 湖南怀化质检]已知乙组人数是甲组人数的一半,若将乙组人数的三分之一调入甲组,则甲组比乙组多 15 人. 则原来甲、乙两组人数分别为 (
A.10 人,5 人
B.12 人,6 人
C.18 人,9 人
D.以上都不对
C
)A.10 人,5 人
B.12 人,6 人
C.18 人,9 人
D.以上都不对
答案:
C 【解析】设原来甲组有 x 人,乙组有 y 人.
根据题意,可列方程组为$\left\{\begin{array}{l} y=\frac {1}{2}x,\\ x+\frac {1}{3}y=\frac {2}{3}y+15,\end{array}\right. $解
得$\left\{\begin{array}{l} x=18,\\ y=9,\end{array}\right. $则原来甲组有 18 人,乙组有 9 人.
根据题意,可列方程组为$\left\{\begin{array}{l} y=\frac {1}{2}x,\\ x+\frac {1}{3}y=\frac {2}{3}y+15,\end{array}\right. $解
得$\left\{\begin{array}{l} x=18,\\ y=9,\end{array}\right. $则原来甲组有 18 人,乙组有 9 人.
2 [2024 山东泰安期末]一服装厂生产一款上衣,已知每米布料可做 1 件衣身或 3 个衣袖,现计划用 45 米这种布料生产这款上衣,设用 $ x $ 米布料做衣身,$ y $ 米布料做衣袖,使得恰好配套(1 件衣身配 2 个衣袖),依题意,可列方程组:
$\left\{\begin{array}{l} x+y=45,\\ 2x=3y\end{array}\right. $
.
答案:
$\left\{\begin{array}{l} x+y=45,\\ 2x=3y\end{array}\right. $【解析】根据题意,可列方程组
为$\left\{\begin{array}{l} x+y=45,\\ 2x=3y.\end{array}\right. $故答案为$\left\{\begin{array}{l} x+y=45,\\ 2x=3y.\end{array}\right. $
为$\left\{\begin{array}{l} x+y=45,\\ 2x=3y.\end{array}\right. $故答案为$\left\{\begin{array}{l} x+y=45,\\ 2x=3y.\end{array}\right. $
3 [2025 上海金山区期末]学生课桌装配车间共有工人 9 名,每名工人每天能装配双人课桌 4 张或者单人椅 10 把. 一张双人课桌与两把单人椅配为一套. 问几名工人装配双人课桌,几名工人装配单人椅才能使每天装配的双人课桌和单人椅刚好配套?
答案:
【解】设 x 名工人装配双人课桌,y 名工人装配
单人椅才能使每天装配的双人课桌和单人椅
刚好配套.
由题意得$\left\{\begin{array}{l} x+y=9,\\ 2×4x=10y,\end{array}\right. $解得$\left\{\begin{array}{l} x=5,\\ y=4.\end{array}\right. $
答:5 名工人装配双人课桌,4 名工人装配单
人椅才能使每天装配的双人课桌和单人椅刚
好配套.
单人椅才能使每天装配的双人课桌和单人椅
刚好配套.
由题意得$\left\{\begin{array}{l} x+y=9,\\ 2×4x=10y,\end{array}\right. $解得$\left\{\begin{array}{l} x=5,\\ y=4.\end{array}\right. $
答:5 名工人装配双人课桌,4 名工人装配单
人椅才能使每天装配的双人课桌和单人椅刚
好配套.
4 [2024 湖南娄底期中]如图所示的长方形中放置了 8 个形状、大小都相同的小长方形,则图中阴影部分的面积为 (
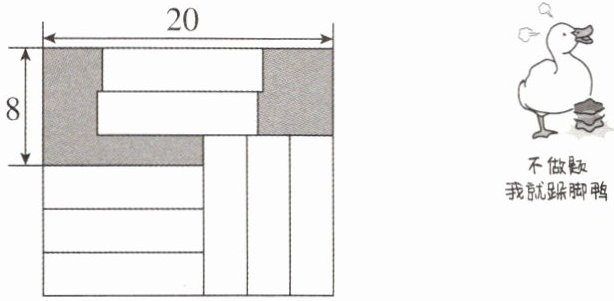
A.33
B.76
C.264
D.340
B
)
A.33
B.76
C.264
D.340
答案:
B 【解析】设小长方形的长为 a,宽为 b. 由题
意知,$\left\{\begin{array}{l} a+3b=20,\\ a-3b+2b=8,\end{array}\right. $解得$\left\{\begin{array}{l} a=11,\\ b=3,\end{array}\right. $所以 8 个小
长方形的面积和为$8×11×3=264$,大长方形的
面积为$(8+3×3)×20=340$,所以阴影部分的
面积为$340-264=76$. 故选 B.
意知,$\left\{\begin{array}{l} a+3b=20,\\ a-3b+2b=8,\end{array}\right. $解得$\left\{\begin{array}{l} a=11,\\ b=3,\end{array}\right. $所以 8 个小
长方形的面积和为$8×11×3=264$,大长方形的
面积为$(8+3×3)×20=340$,所以阴影部分的
面积为$340-264=76$. 故选 B.
5 [2024 湖南郴州期末]自来水厂的供水池分别有 7 个进出水口,每天早晨 6 点开始进出水,且此时水池中有水 15%,在每个进出水口是匀速进出的情况下,如果开放 3 个进口和 4 个出口,5 小时将水池注满;如果开放 4 个进口和 3 个出口,2 小时将水池注满. 若某一天早晨 6 点时水池中有水 24%,又因为水管改造,只能开放 3 个进口和 2 个出口,则从早晨 6 点开始经过
$\frac {38}{17}$
小时,水池的水刚好注满.
答案:
$\frac {38}{17}$【解析】设每个进水口每小时的进水量
为 x,每个出水口每小时的出水量为 y. 依题意,
得$\left\{\begin{array}{l} 5(3x-4y)=1-15\% ,\\ 2(4x-3y)=1-15\% ,\end{array}\right. $解得$\left\{\begin{array}{l} x=0.17=17\% ,\\ y=0.085=8.5\% ,\end{array}\right. $
所以$\frac {1-24\% }{3×17\% -2×8.5\% }=\frac {38}{17}$(时). 故答案为$\frac {38}{17}.$
为 x,每个出水口每小时的出水量为 y. 依题意,
得$\left\{\begin{array}{l} 5(3x-4y)=1-15\% ,\\ 2(4x-3y)=1-15\% ,\end{array}\right. $解得$\left\{\begin{array}{l} x=0.17=17\% ,\\ y=0.085=8.5\% ,\end{array}\right. $
所以$\frac {1-24\% }{3×17\% -2×8.5\% }=\frac {38}{17}$(时). 故答案为$\frac {38}{17}.$
6 [2024 安徽合肥庐阳区校级期末]某鞋店正举办开学特惠活动,如图为活动说明. 小李打算在该店一次性购买两双价格不同的鞋,且他有一张所有购买的商品皆打 8 折的折价券.
(1)若小李参加特惠活动需花费 420 元,比使用折价券多花 20 元,则两双鞋的原价分别为多少元?
(2)若小李计算后发现使用折价券与参加特惠活动两者的花费相差 60 元,则两双鞋的原价相差多少元?

(1)若小李参加特惠活动需花费 420 元,比使用折价券多花 20 元,则两双鞋的原价分别为多少元?
(2)若小李计算后发现使用折价券与参加特惠活动两者的花费相差 60 元,则两双鞋的原价相差多少元?

答案:
【解】
(1)设两双鞋的原价分别为 x 元和 y 元,
且$x>y$. 由题意得$\left\{\begin{array}{l} x+0.6y=420,\\ 0.8x+0.8y=420-20,\end{array}\right. $
解得$\left\{\begin{array}{l} x=300,\\ y=200.\end{array}\right. $
答:两双鞋的原价分别为 300 元和 200 元.
(2)设两双鞋的原价分别为 a 元和 b 元,且$a>b.$
①当使用折价券比参加特惠活动多花费 60
元时,由题意得$(0.8a+0.8b)-(a+0.6b)=60$,整理得$b-a=300$,与$a>b$矛盾,此情况不成立.
②当参加特惠活动比使用折价券多花费 60
元时,由题意得$(a+0.6b)-(0.8a+0.8b)=60$,整理得$a-b=300.$
答:两双鞋的原价相差 300 元.
(1)设两双鞋的原价分别为 x 元和 y 元,
且$x>y$. 由题意得$\left\{\begin{array}{l} x+0.6y=420,\\ 0.8x+0.8y=420-20,\end{array}\right. $
解得$\left\{\begin{array}{l} x=300,\\ y=200.\end{array}\right. $
答:两双鞋的原价分别为 300 元和 200 元.
(2)设两双鞋的原价分别为 a 元和 b 元,且$a>b.$
①当使用折价券比参加特惠活动多花费 60
元时,由题意得$(0.8a+0.8b)-(a+0.6b)=60$,整理得$b-a=300$,与$a>b$矛盾,此情况不成立.
②当参加特惠活动比使用折价券多花费 60
元时,由题意得$(a+0.6b)-(0.8a+0.8b)=60$,整理得$a-b=300.$
答:两双鞋的原价相差 300 元.
查看更多完整答案,请扫码查看


