《2025年初中必刷题七年级数学上册湘教版》

11 [2024 湖南衡阳期末]把 1 ~ 9 这九个数填入 $ 3×3 $ 的方格中,使其每一横行,每一竖列以及两条斜对角线上的 3 个数之和都相等(记这个和为 $ a $),这样便构成了一个“九宫格”,它源于我国古代的“洛书”,是世界上最早的“幻方”,图(1)是仅可以看到部分数值的“九宫格”,我们尝试解决下列问题：

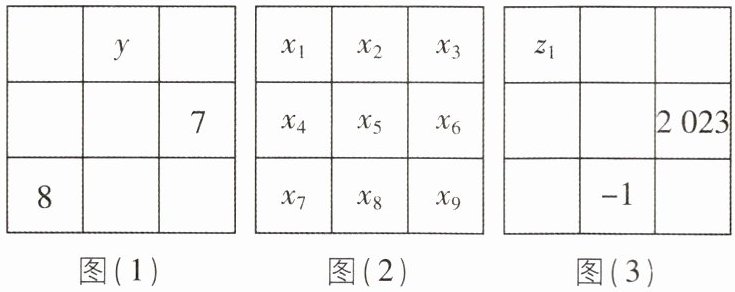
(1)1 ~ 9 这九个数的和是______,所以每一横行的 3 个数之和 $ a $ 等于______；
(2)如图(2),$ x_1 + x_5 + x_9 = a $,$ x_3 + x_5 + x_7 = a $,$ x_2 + x_5 + x_8 = a $,$ x_4 + x_5 + x_6 = a $,将这四个式子相加后代入 $ x_1 + x_2 + x_3 + x_4 + x_5 + x_6 + x_7 + x_8 + x_9 $ 的值,可求得 $ x_5 = $______,结合图(1)可依次填满其余空格,故图(1)中 $ y = $______；
(3)如图(3),将 1 ~ 9 改为其他 9 个整数,其余要求不变,请求出图(3)中的 $ z_1 $.

答案：
11.【解】
(1)因为1 + 2 + 3 + … + 9 = 45,所以每一横行的3个数之和a等于45÷3 = 15,故答案为45,15.
(2)由题意可得(x1 + x5 + x9) + (x3 + x5 + x7) + (x2 + x5 + x8) + (x4 + x5 + x6) = x1 + x2 + x3 + x4 + x5 + x6 + x7 + x8 + x9 + 3x5 = 4a,所以45 + 3x5 = 4×15,所以x5 = 5,故将题图
(1)填满如图
(1)所示: 则y = 9,故答案为5,9.
(3)如图
(2),由(z1 + z2 + z3) + (z1 + z5 + z9) = (z2 + z5 - 1) + (z3 + 2023 + z9),得2z1 = - 1 + 2023,所以z1 = 1011.

12 [2025 黑龙江哈尔滨期中]哈尔滨亚冬会的某个比赛场馆装修后产生的建筑垃圾需要清理,计划租用甲、乙两车队清理建筑垃圾,已知甲车队单独运完需要 20 天,乙车队单独运完需要 30 天. 现乙车队先单独运了 5 天,然后甲、乙两车队合作运完剩下的垃圾.
(1)甲、乙两车队合作还需要多少天运完剩下的垃圾？
(2)已知甲车队每天的租金为 170 元,比乙车队多 30 元,运完垃圾后共需支付甲、乙两车队租金多少元？

答案： 12.【解】
(1)设甲、乙两车队合作还需要x天运完剩下的垃圾.根据题意得$\frac{5}{30}$ + $\frac{x}{20}$ + $\frac{x}{30}$ = 1,解得x = 10.答:甲、乙两车队合作还需要10天运完剩下的垃圾.
(2)乙车队一共工作了15天,甲车队一共工作了10天,(170 - 30)×15 + 170×10 = 3800(元).答:运完垃圾后共需支付甲、乙两车队租金3800元.

13 [2024 湖南长沙期末]我们规定,若关于 $ x $ 的一元一次方程 $ ax = b (a ≠ 0) $ 的解为 $ x = a - b $,则称该方程为“天心方程”. 例如,$ 2x = \frac{4}{3} $ 的解为 $ x = \frac{2}{3} $,而 $ 2 - \frac{4}{3} = \frac{2}{3} $,则该方程 $ 2x = \frac{4}{3} $ 就是“天心方程”. 请根据上述规定解答下列问题：
(1)一元一次方程 $ 2x = 4 $______(填“是”或“不是”)“天心方程”.
(2)若关于 $ x $ 的一元一次方程 $ 4x = c $ 是“天心方程”,则 $ c = $______.
(3)若关于 $ x $ 的一元一次方程 $ 3x = a + ab (a ≠ 0) $ 是“天心方程”,且它的解为 $ x = a $,求 $ a $,$ b $ 的值.
(4)若关于 $ x $ 的一元一次方程 $ x = 3m - mn $ 和关于 $ y $ 的一元一次方程 $ -3y = mn - 2n $ 都是“天心方程”,求代数式 $ 2(mn - 3n) + \frac{1}{3}(33m - 8mn) - \frac{1}{3} $ 的值.
(1)不是
(2)$\frac{16}{5}$
(3)由方程$3x = a + ab$解得$x = \frac{a + ab}{3}$，因为解为$x = a$，所以$\frac{a + ab}{3}=a$①；又因是“天心方程”，所以$3-(a + ab)=a$②，联立①②解得$a = \frac{3}{4}$，$b = 2$
(4)由$x = 3m - mn$是“天心方程”得$1-(3m - mn)=3m - mn$，即$3m - mn=\frac{1}{2}$①；由$-3y = mn - 2n$是“天心方程”得$-3-(mn - 2n)=-\frac{1}{3}(mn - 2n)$，即$mn - 2n=-\frac{9}{2}$②，联立①②得$3m - 2n=-4$，代入代数式计算得$-12$

答案： 13.【解】
(1)2x = 4,解得x = 2.因为2 - 4 = - 2 ≠ 2,所以2x = 4不是“天心方程”,故答案为不是.
(2)4x = c,解得x = $\frac{c}{4}$.因为一元一次方程4x = c是“天心方程”,所以4 - c = $\frac{c}{4}$,解得c = $\frac{16}{5}$,故答案为$\frac{16}{5}$.
(3)3x = a + ab(a ≠ 0),解得x = $\frac{a + ab}{3}$.因为方程的解为x = a,所以$\frac{a + ab}{3}$ = a.①因为一元一次方程3x = a + ab(a ≠ 0)是“天心方程”,所以3 - (a + ab) = a,②联立①②,解得{a = $\frac{3}{4}$, b = 2,故a = $\frac{3}{4}$,b = 2.
(4)因为一元一次方程x = 3m - mn是“天心方程”,所以1 - (3m - mn) = 3m - mn,所以3m - mn = $\frac{1}{2}$.①因为关于y的一元一次方程 - 3y = mn - 2n是“天心方程”,所以y = - $\frac{1}{3}$(mn - 2n),所以 - 3 - (mn - 2n) = - $\frac{1}{3}$(mn - 2n),所以mn - 2n = - $\frac{9}{2}$,②由①②得3m - 2n = - 4,③ mn = 3m - $\frac{1}{2}$,④ mn = - $\frac{9}{2}$ + 2n,⑤将③④⑤代入代数式得,原式 = 2(- $\frac{9}{2}$ + 2n - 3n) + $\frac{1}{3}$[33m - 8(3m - $\frac{1}{2}$)] - $\frac{1}{3}$ = - 9 - 2n + $\frac{1}{3}$(9m + 4) - $\frac{1}{3}$ = - 9 - 2n + 3m + $\frac{4}{3}$ - $\frac{1}{3}$ = 3m - 2n - 8 = - 4 - 8 = - 12.