《2025年初中必刷题七年级数学上册湘教版》

1 [2024 贵州中考] 计算 $ 2a + 3a $ 的结果正确的是(A)
A.$ 5a $
B.$ 6a $
C.$ 5a^{2} $
D.$ 6a^{2} $

答案： A 【解析】2a+3a=(2+3)a=5a.

2 [2024 湖南娄底期末] 下列说法中,正确的是(C)
A.多项式 $ a^{2}+2a^{2}b + 3 $ 是二次三项式
B.单项式 $ -\pi x^{2}y $ 的系数是 -1
C.单项式 $ 4m^{2}n $ 和 $ -nm^{2} $ 是同类项
D.$ ab + 3b $ 是单项式

答案： C 【解析】多项式a²+2a²b+3是三次三项式,故选项A错误;单项式-πx²y的系数是-π,故选项B错误;单项式4m²n和-nm²是同类项,故选项C正确;ab+3b是多项式,故选项D错误.故选C.

3 [2024 云南昭通质检] 一组数：2,1,5,$ x $,17,$ y $,65,满足“前两个数依次为 $ a $,$ b $,紧随其后的第三个数是 $ 2a + b $”,例如这组数中的第三个数“5”是由“$ 2×2 + 1 $”得到的,那么这组数中 $ y $ 表示的数为(C)
A.27
B.11
C.31
D.41

答案： C 【解析】依题意,得x=2×1+5=7,y=2×7+17=31,故选C.

4 [2024 广东广州中考] 若 $ a^{2}-2a - 5 = 0 $,则 $ 2a^{2}-4a + 1 = $11。

答案： 11 【解析】因为a²-2a-5=0,所以a²-2a=5,所以原式=2(a²-2a)+1=2×5+1=11,故答案为11.

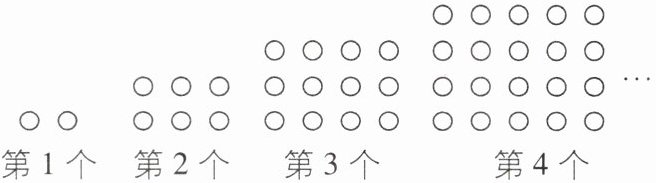
5 [2024 西藏中考] 如图是由若干个大小相同的“○”组成的一组有规律的图案,其中第 1 个图案用了 2 个“○”,第 2 个图案用了 6 个“○”,第 3 个图案用了 12 个“○”,第 4 个图案用了 20 个…“○”,,依照此规律,第 $ n $ 个图案中“○”的个数为n²+n(用含 $ n $ 的代数式表示)。

答案： n²+n 【解析】由所给图形可知第1个图案中“○”的个数为2=1×2;第2个图案中“○”的个数为6=2×3;第3个图案中“○”的个数为12=3×4;…,所以第n个图案中“○”的个数为n(n+1)=n²+n.故答案为n²+n.

6 [2024 湖南岳阳期中] 先化简,再求值：若 $ (x - 3)^{2}+\vert y + 2\vert = 0 $,求代数式 $ 3x^{2}y - [xy^{2}-2(2xy^{2}-3x^{2}y)+x^{2}y]+4xy^{2} $ 的值。

答案： 【解】因为(x-3)²+|y+2|=0,(x-3)²≥0,|y+2|≥0,所以(x-3)²=0,|y+2|=0,所以x-3=0,y+2=0,所以x=3,y=-2.原式=3x²y-(xy²-4xy²+6x²y+x²y)+4xy²=3x²y-xy²+4xy²-6x²y-x²y+4xy²=-4x²y+7xy².当x=3,y=-2时,原式=-4×3²×(-2)+7×3×(-2)²=72+84=156.

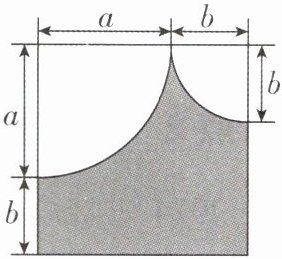
7 [2024 湖南郴州期中] 如图,正方形中有两个四分之一圆。
(1)用代数式表示阴影部分的面积；
(2)当 $ a = 2 $,$ b = 1 $ 时,阴影部分的面积是多少(结果保留 $ \pi $)？

答案： 【解】
(1)由题意得,阴影部分的面积为$(a+b)²-\frac{1}{4}πa²-\frac{1}{4}πb². (2)$当a=2,b=1时,阴影部分的面积为$(a+b)²-\frac{1}{4}πa²-\frac{1}{4}πb²=(2+1)²-\frac{1}{4}×π×2²-\frac{1}{4}×π×1²=9-π-\frac{1}{4}π=9-\frac{5}{4}π.$

8 [2024 北京海淀区期中] 有一种计算器,输出规则如下：输入两个关于 $ x $ 的整式 $ A $,$ B $,对它们进行整式加法运算,若 $ A + B $ 的结果为单项式,则输出该单项式；若 $ A + B $ 的结果为多项式,则输出该多项式的最高次项与最低次项的和。已知输入的整式 $ A = x^{2}+x - 2 $。
(1)若 $ B = 3x^{2}-4 $,则输出结果为4x²-6。
(2)若输出结果为 $ 3x^{3}-x $,则整式 $ B $ 应满足什么条件？写出结论,并说明理由。
(3)若将整式 $ A $,$ B $ 输入计算器,得到输出结果,记为第一次运算；将输出结果与 $ A $ 再次输入该计算器,得到输出结果,记为第二次运算；…。依次进行上面操作,若第 $ n(n\geq3) $ 次运算得到的输出结果恰为单项式,请写出一个满足题意的整式 $ B $。

答案： 【解】
(1)由题意得A+B=x²+x-2+3x²-4=4x²+x-6,所以A+B的结果为多项式,所以输出的结果为4x²-6.故答案为4x²-6.
(2)整式B=3x³+bx²-2x+2(b为任意常数).理由如下:由A+B的输出结果为3x³-x,且A=x²+x-2可知整式B含有3x³,且常数项为2,含x的一次项系数为-2,对于含不含x的二次项无法确定,所以整式B=3x³+bx²-2x+2(b为任意常数).
(3)满足题意的整式B为-3x²+6(答案不唯一).x²+x-2+(-3x²+6)=x²+x-2-3x²+6=-2x²+x+4,第一次运算输出结果为-2x²+4;x²+x-2+(-2x²+4)=x²+x-2-2x²+4=-x²+x+2,第二次运算输出结果为-x²+2;x²+x-2+(-x²+2)=x²+x-2-x²+2=x,第三次运算输出结果为x.符合题意.