第79页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
1 [中]如图,已知点 $ C $ 为线段 $ AB $ 的中点,$ D $ 为 $ CB $ 上一点,下列关系表示错误的是(
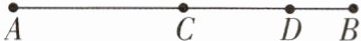
A.$ CD = AC - DB $
B.$ BD + AC = 2BC - CD $
C.$ 2CD = 2AD - AB $
D.$ AB - CD = AC - BD $
D
)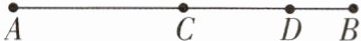
A.$ CD = AC - DB $
B.$ BD + AC = 2BC - CD $
C.$ 2CD = 2AD - AB $
D.$ AB - CD = AC - BD $
答案:
D 【解析】因为点 C 是线段 AB 的中点,所以AC=BC,AB=2BC=2AC,所以CD=BC - BD=AC - BD,所以选项 A 正确,不符合题意;因为BD+AC=AB - CD=2BC - CD,所以选项 B 正确,不符合题意;因为CD=AD - AC,所以2CD=2AD - 2AC=2AD - AB,所以选项 C 正确,不符合题意.而选项 D 中,AB - CD=AC+BD,所以选项 D 错误,符合题意.故选 D.
2 [2024 湖南永州期末,中]如图,$ A,B,C $ 为直线 $ l $ 上从左到右的三个点,$ AB = 2BC $,动点 $ M,N $ 分别从 $ A,B $ 两点同时出发,向右运动,点 $ M $ 的速度是点 $ N $ 的速度的 $ 3 $ 倍。在运动过程中,若要知道 $ MN $ 的长,则只要知道一条线段的长即可,该线段是(

A.$ AM $
B.$ BN $
C.$ BM $
D.$ CM $
D
)
A.$ AM $
B.$ BN $
C.$ BM $
D.$ CM $
答案:
D 【解析】设BC=a,则AB=2a.因为动点M,N 分别从A,B 两点同时出发,向右运动,点 M 的速度是点 N 的速度的 3 倍,所以AM=3BN.设BN=b,则AM=3b,所以MN=|AB+BN - AM|=|2a+b - 3b|=|2a - 2b|,BM=|AB - AM|=|2a - 3b|,CM=|AB+BC - AM|=|3a - 3b|,所以MN=$\frac{2}{3}$CM.故选 D.
3 [2025 湖南长沙期末,中]一条水平直线 $ l $ 上有 $ A,B,C $ 三点,$ AB = 12\ cm,AC = 2BC $,$ D $ 为 $ BC $ 的中点,则 $ AD $ 的长为______。
答案:
10 cm 或 18 cm 【解析】根据题意,分两种情况:①当点 C 在线段 AB 上时,如图
(1).

因为AB=12 cm,AC=2BC,所以AC+BC=2BC+BC=3BC=12 cm,所以BC=4 cm,所以AC=8 cm.因为 D 为 BC 的中点,所以CD=$\frac{1}{2}$BC=2 cm,所以AD=AC+CD=8+2=10(cm).②当点 C 在线段 AB 的延长线上时,如图
(2).

因为AB=12 cm,AC=2BC,所以BC=AB=12 cm.因为 D 为 BC 的中点,所以BD=$\frac{1}{2}$BC=6 cm,所以AD=AB+BD=12+6=18(cm).综上所述,AD 的长为 10 cm 或 18 cm.故答案为 10 cm 或 18 cm.
10 cm 或 18 cm 【解析】根据题意,分两种情况:①当点 C 在线段 AB 上时,如图
(1).

因为AB=12 cm,AC=2BC,所以AC+BC=2BC+BC=3BC=12 cm,所以BC=4 cm,所以AC=8 cm.因为 D 为 BC 的中点,所以CD=$\frac{1}{2}$BC=2 cm,所以AD=AC+CD=8+2=10(cm).②当点 C 在线段 AB 的延长线上时,如图
(2).

因为AB=12 cm,AC=2BC,所以BC=AB=12 cm.因为 D 为 BC 的中点,所以BD=$\frac{1}{2}$BC=6 cm,所以AD=AB+BD=12+6=18(cm).综上所述,AD 的长为 10 cm 或 18 cm.故答案为 10 cm 或 18 cm.
4 [2024 安徽安庆期末,中]如图所示,$ B $ 在线段 $ AC $ 上,且 $ BC = 3AB $,$ D $ 是线段 $ AB $ 的中点,$ E $ 是线段 $ BC $ 上的一点,$ BE:EC = 2:1 $,则下列结论:① $ EC = \dfrac{1}{3}AE $;② $ DE = 5BD $;③ $ BE = \dfrac{1}{2}(AE + BC) $;④ $ AE = \dfrac{6}{5}(BC - AD) $,其中结论正确的有______

①②④
。(填序号)
答案:
①②④ 【解析】因为 E 是线段 BC 上的一点,BE:EC=2:1,BC=3AB,所以EC=$\frac{1}{3}$BC,AB=$\frac{1}{3}$BC,所以AB=EC,所以AB+BE=EC+BE,所以AE=BC,所以EC=$\frac{1}{3}$AE,故①正确;因为EC=$\frac{1}{3}$AE,所以AE=3EC.因为AB=EC,所以AE=3AB.因为 D 是线段 AB 的中点,所以AD=BD=$\frac{1}{2}$AB,所以DE=AE - AD=3AB - $\frac{1}{2}$AB=$\frac{5}{2}$AB,所以DE=$\frac{5}{2}$×2BD=5BD,故②正确;因为BC=3AB,AE=3AB,所以$\frac{1}{2}$(AE+BC)=$\frac{1}{2}$(3AB+3AB)=3AB.因为BE=AE - AB=3AB - AB=2AB,所以$\frac{BE}{\frac{1}{2}(AE+BC)}$=$\frac{2AB}{3AB}$=$\frac{2}{3}$,所以BE=$\frac{2}{3}$×$\frac{1}{2}$(AE+BC)=$\frac{1}{3}$(AE+BC),故③不正确;因为BC=3AB,AD=$\frac{1}{2}$AB,所以$\frac{6}{5}$(BC - AD)=$\frac{6}{5}$(3AB - $\frac{1}{2}$AB)=3AB.因为AE=3AB,所以AE=$\frac{6}{5}$(BC - AD),故④正确.综上,正确的有①②④.故答案为①②④.
5 [2025 江西吉安期末,难]如图,将一段长为 $ 11\ cm $ 的绳子 $ AB $ 拉直铺平后折叠(绳子无弹性,折叠处长度忽略不计),使绳子与自身一部分重叠。若将绳子 $ AB $ 沿 $ N $ 点折叠后,点 $ B $ 落在 $ B' $ 处(点 $ B' $ 始终在点 $ A $ 右侧),在重合部分 $ B'N $ 上沿绳子垂直方向剪断,将绳子分为三段,若这三段的长度由短到长的比为 $ 2:3:6 $,则 $ BN $ 的长度为______。
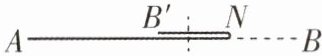
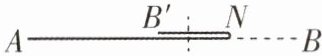
答案:
3.5 cm 或 4 cm 或 5 cm 【解析】设绳子三段的长度分别为 2x cm、3x cm 和 6x cm,两个断点分别为 F,E,则2x+3x+6x=11,解得x=1.①若AF=3x,FE=6x,EB=2x,如图
(1).

因为 N 为 EF 的中点,所以NE=$\frac{1}{2}$EF=3x,所以BN=3x+2x=5x=5.②若AF=6x,FE=3x,EB=2x,如图
(2).

因为 N 为 EF 的中点,所以NE=$\frac{1}{2}$EF=1.5x,所以BN=1.5x+2x=3.5x=3.5.③若AF=6x,FE=2x,EB=3x,如图
(3).

因为 N 为 EF 的中点,所以NE=$\frac{1}{2}$EF=x,所以BN=x+3x=4x=4.故答案为 3.5 cm 或 4 cm 或 5 cm.
3.5 cm 或 4 cm 或 5 cm 【解析】设绳子三段的长度分别为 2x cm、3x cm 和 6x cm,两个断点分别为 F,E,则2x+3x+6x=11,解得x=1.①若AF=3x,FE=6x,EB=2x,如图
(1).

因为 N 为 EF 的中点,所以NE=$\frac{1}{2}$EF=3x,所以BN=3x+2x=5x=5.②若AF=6x,FE=3x,EB=2x,如图
(2).

因为 N 为 EF 的中点,所以NE=$\frac{1}{2}$EF=1.5x,所以BN=1.5x+2x=3.5x=3.5.③若AF=6x,FE=2x,EB=3x,如图
(3).

因为 N 为 EF 的中点,所以NE=$\frac{1}{2}$EF=x,所以BN=x+3x=4x=4.故答案为 3.5 cm 或 4 cm 或 5 cm.
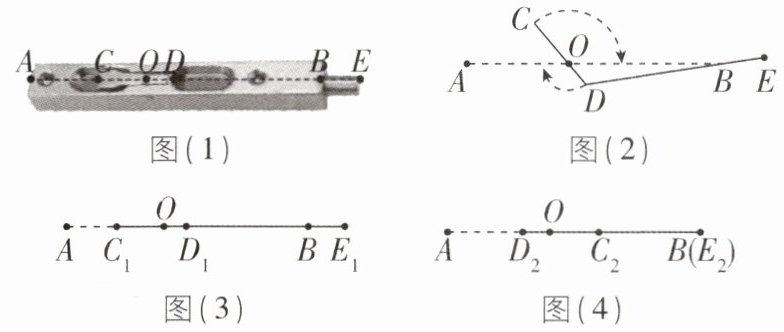
6 [2024 浙江温州期末,较难]如图(1),一款暗插销由外壳 $ AB $,开关 $ CD $,锁芯 $ DE $ 三部分组成,其工作原理如图(2),开关 $ CD $ 绕固定点 $ O $ 转动,由连接点 $ D $ 带动锁芯 $ DE $ 移动。图(3)为插销开启状态,此时连接点 $ D $ 在线段 $ AB $ 上,如 $ D_1 $ 位置。开关 $ CD $ 绕点 $ O $ 顺时针旋转 $ 180° $ 后得到 $ C_2D_2 $,锁芯弹回至 $ D_2E_2 $ 位置(点 $ B $ 与点 $ E_2 $ 重合),此时插销闭合,如图(4)。已知 $ CD = 74\ mm,AD_2 - AC_1 = 50\ mm $,则 $ BE_1 = $
24
$ mm $。
答案:
24 【解析】由题图
(3)得OB=OD₁+D₁E₁ - BE₁,由题图
(4)得OB=D₂E₂ - OD₂.由题意得D₁E₁=D₂E₂,OD₁=OD₂,所以BE₁=OD₁+OD₂=2OD₂.因为AD₂ - AC₁=50,所以(AO - OD₂) - (AO - OC₁)=50,所以OC₁ - OD₂=50,所以OC₁=OD₂+50.因为OC=OC₁,所以CD=OC+OD=OC₁+OD₁=OC₁+OD₂=OD₂+50+OD₂=74,所以2OD₂=24,所以BE₁=24 mm.故答案为 24.
(3)得OB=OD₁+D₁E₁ - BE₁,由题图
(4)得OB=D₂E₂ - OD₂.由题意得D₁E₁=D₂E₂,OD₁=OD₂,所以BE₁=OD₁+OD₂=2OD₂.因为AD₂ - AC₁=50,所以(AO - OD₂) - (AO - OC₁)=50,所以OC₁ - OD₂=50,所以OC₁=OD₂+50.因为OC=OC₁,所以CD=OC+OD=OC₁+OD₁=OC₁+OD₂=OD₂+50+OD₂=74,所以2OD₂=24,所以BE₁=24 mm.故答案为 24.
7 [2025 河南濮阳质检,较难]如图,点 $ M $ 在线段 $ AN $ 的延长线上,且线段 $ MN = 16 $,第一次操作:分别取线段 $ AM $ 和 $ AN $ 的中点 $ M_1,N_1 $;第二次操作:分别取线段 $ AM_1 $ 和 $ AN_1 $ 的中点 $ M_2,N_2 $;第三次操作:分别取线段 $ AM_2 $ 和 $ AN_2 $ 的中点 $ M_3,N_3 $;…$$,连续这样操作 $ 4 $ 次,则 $ M_4N_4 = $
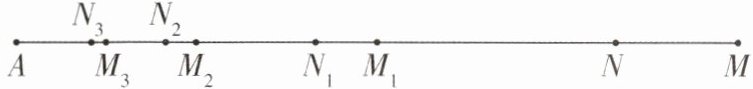
1
。
答案:
1 【解析】因为MN=16,所以AM - AN=MN=16.因为线段AM 和 AN 的中点分别为M₁,N₁,所以M₁N₁=AM₁ - AN₁=$\frac{AM}{2}$ - $\frac{AN}{2}$=$\frac{AM - AN}{2}$=$\frac{1}{2}$MN.同理可得M₂N₂=AM₂ - AN₂=$\frac{AM₁}{2}$ - $\frac{AN₁}{2}$=$\frac{AM₁ - AN₁}{2}$=$\frac{1}{2}$M₁N₁=($\frac{1}{2}$)²MN,所以M₃N₃=($\frac{1}{2}$)³MN,所以M₄N₄=($\frac{1}{2}$)⁴MN=($\frac{1}{2}$)⁴×16=1,故答案为 1.
8 [2024 湖南张家界期末,中]如图,三角形 $ ABC $,$ BC = a,AC = b,AB = c $,点 $ D $ 为线段 $ AB $ 的中点。
(1)请在线段 $ AC $ 上,用圆规作出线段 $ CE = b - \dfrac{1}{2}c $;
(2)请在线段 $ BC $ 上,用圆规作出线段 $ BF = a - b + \dfrac{1}{2}c $。
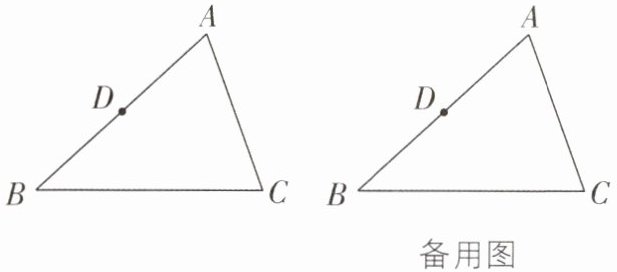
(1)请在线段 $ AC $ 上,用圆规作出线段 $ CE = b - \dfrac{1}{2}c $;
(2)请在线段 $ BC $ 上,用圆规作出线段 $ BF = a - b + \dfrac{1}{2}c $。

答案:
【解】
(1)如图,CE 即为所作.
(2)如图,BF 即为所作.

【解】
(1)如图,CE 即为所作.
(2)如图,BF 即为所作.

9 [2025 湖南怀化期末,较难]如图,$ M $ 是线段 $ AB $ 上一定点,$ C,D $ 两点分别从 $ M,B $ 出发,分别以 $ 1\ cm/s,3\ cm/s $ 的速度沿 $ BA $ 方向运动($ C $ 在线段 $ AM $ 上,$ D $ 在线段 $ BM $ 上)。
(1)若 $ AB = 10\ cm $,当点 $ C,D $ 运动 $ 1\ s $ 时,求 $ AC + MD $ 的值;
(2)若点 $ C,D $ 运动时,总有 $ MD = 3AC $,则 $ AM = $______$ AB $;
(3)在(2)的条件下,$ N $ 是直线 $ AB $ 上一点,且 $ AN - BN = MN $,求 $ \dfrac{MN}{AB} $ 的值。
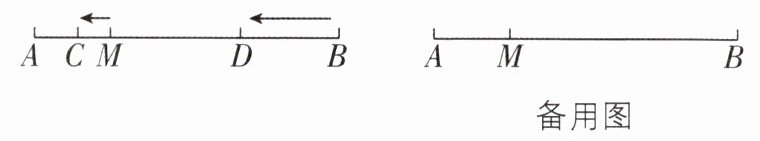
(1)若 $ AB = 10\ cm $,当点 $ C,D $ 运动 $ 1\ s $ 时,求 $ AC + MD $ 的值;
(2)若点 $ C,D $ 运动时,总有 $ MD = 3AC $,则 $ AM = $______$ AB $;
(3)在(2)的条件下,$ N $ 是直线 $ AB $ 上一点,且 $ AN - BN = MN $,求 $ \dfrac{MN}{AB} $ 的值。
答案:
【解】
(1)当点 C,D 运动 1 s 时,CM=1 cm,BD=3 cm.因为AB=10 cm,所以AC+MD=AB - CM - BD=10 - 1 - 3=6(cm).
(2)$\frac{1}{4}$ 【解析】设运动时间为 t s,则CM=t cm,BD=3t cm,所以BD=3CM.因为AC=AM - CM,MD=BM - BD,MD=3AC,所以BM - BD=3AM - 3CM,即BM=3AM.因为BM=AB - AM,所以AB - AM=3AM,所以AM=$\frac{1}{4}$AB.故答案为$\frac{1}{4}$.
(3)①当点 N 在线段 AB 上时,如图
(1).

因为AN - BN=MN,AN - AM=MN,所以BN=AM=$\frac{1}{4}$AB,所以MN=AB - AM - BN=$\frac{1}{2}$AB,即$\frac{MN}{AB}$=$\frac{1}{2}$.②当点 N 在线段 AB 的延长线上时,如图
(2).

因为AN - BN=MN,AN - BN=AB,所以MN=AB,即$\frac{MN}{AB}$=1.综上所述,$\frac{MN}{AB}$的值为$\frac{1}{2}$或 1.
【解】
(1)当点 C,D 运动 1 s 时,CM=1 cm,BD=3 cm.因为AB=10 cm,所以AC+MD=AB - CM - BD=10 - 1 - 3=6(cm).
(2)$\frac{1}{4}$ 【解析】设运动时间为 t s,则CM=t cm,BD=3t cm,所以BD=3CM.因为AC=AM - CM,MD=BM - BD,MD=3AC,所以BM - BD=3AM - 3CM,即BM=3AM.因为BM=AB - AM,所以AB - AM=3AM,所以AM=$\frac{1}{4}$AB.故答案为$\frac{1}{4}$.
(3)①当点 N 在线段 AB 上时,如图
(1).

因为AN - BN=MN,AN - AM=MN,所以BN=AM=$\frac{1}{4}$AB,所以MN=AB - AM - BN=$\frac{1}{2}$AB,即$\frac{MN}{AB}$=$\frac{1}{2}$.②当点 N 在线段 AB 的延长线上时,如图
(2).

因为AN - BN=MN,AN - BN=AB,所以MN=AB,即$\frac{MN}{AB}$=1.综上所述,$\frac{MN}{AB}$的值为$\frac{1}{2}$或 1.
查看更多完整答案,请扫码查看


