第53页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
1. 新考法 [较难]如图,正方形$ABCD$的轨道上有甲、乙两个点,开始时甲在$A$处,乙在$C$处,它们沿着正方形轨道顺时针运动且同时出发,甲的速度为每秒$1cm$,乙的速度为每秒$5cm$。已知正方形轨道$ABCD的边长为2cm$,则乙在第2022次追上甲时的位置在(
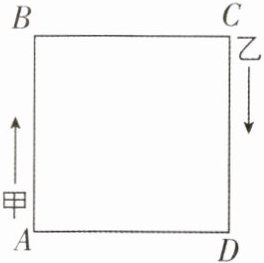
A.$AB$上
B.$BC$上
C.$CD$上
D.$AD$上
B
)
A.$AB$上
B.$BC$上
C.$CD$上
D.$AD$上
答案:
B 【解析】设乙走x秒第一次追上甲.根据题意,得5x-x=4,解得x=1,所以乙走1秒第1次追上甲,则乙在第1次追上甲时的位置在AB上.设乙再走y秒第2次追上甲.根据题意,得5y-y=8,解得y=2,所以乙再走2秒第2次追上甲,则乙在第2次追上甲时的位置在BC上.同理,乙再走2秒第3次追上甲,则乙在第3次追上甲时的位置在CD上;乙再走2秒第4次追上甲,则乙在第4次追上甲时的位置在DA上;乙在第5次追上甲时的位置又回到AB上.因为2022÷4=505……2,所以乙在第2022次追上甲时的位置在BC上.故选B.
2. [2025上海徐汇区质检,中]在一段1000米长的比赛道路上,自东向西每隔5米安排一位志愿者,自东向西每隔6米安排一位保安。若志愿者与保安之间间隔1米,则在此处放置一个标志牌,问这段道路上要放置多少个标志牌?
答案:
【解】5和6的最小公倍数是5×6=30,30以内5的倍数有5,10,15,20,25,30,30以内6的倍数有6,12,18,24,30.因为6-5=1,25-24=1,所以每30米放置标志牌的个数是2个.1000以内30的最大倍数是990,则设这990米道路上一共放置x个标志牌.由题意可得$\dfrac{x}{2}=\dfrac{990}{30},$解得x=66.余下的10米内还要放置1个标志牌,则66+1=67(个).答:这段道路上要放置67个标志牌.
3. [2024浙江杭州期末,较难]学校组织植树活动,已知在甲处植树的有220人,在乙处植树的有96人。
(1)若要使甲处植树的人数是乙处植树人数的3倍,应从乙处调多少人去甲处?
(2)为了尽快完成植树任务,现调$m$人去两处支援,其中$90<m<100$,若要使甲处植树的人数仍然是乙处植树人数的3倍,则应调往甲、乙两处各多少人?
(1)若要使甲处植树的人数是乙处植树人数的3倍,应从乙处调多少人去甲处?
(2)为了尽快完成植树任务,现调$m$人去两处支援,其中$90<m<100$,若要使甲处植树的人数仍然是乙处植树人数的3倍,则应调往甲、乙两处各多少人?
答案:
(1)设应从乙处调x人去甲处.根据题意得220+x=3(96-x),解得x=17.答:应从乙处调17人去甲处.
(2)设调往甲处y人,甲处现有(220+y)人,则调往乙处(m-y)人,乙处现有(96+m-y)人.根据题意得220+y=3(96+m-y),所以$y=\dfrac{68+3m}{4}.$因为90<m<100,y<m,且m,y均为整数,所以当m=91时$,y=\dfrac{68+3m}{4}=\dfrac{341}{4}($舍去);当m=92时$,y=\dfrac{68+3m}{4}=\dfrac{344}{4}=86;$当m=93时$,y=\dfrac{68+3m}{4}=\dfrac{347}{4}($舍去);当m=94时$,y=\dfrac{68+3m}{4}=\dfrac{350}{4}=\dfrac{175}{2}($舍去);当m=95时$,y=\dfrac{68+3m}{4}=\dfrac{353}{4}($舍去);当m=96时$,y=\dfrac{68+3m}{4}=\dfrac{356}{4}=89;$当m=97时$,y=\dfrac{68+3m}{4}=\dfrac{359}{4}($舍去);当m=98时$,y=\dfrac{68+3m}{4}=\dfrac{362}{4}=\dfrac{181}{2}($舍去);当m=99时$,y=\dfrac{68+3m}{4}=\dfrac{365}{4}($舍去).综上所述,当m=92时,应调往甲处86人,乙处6人;当m=96时,应调往甲处89人,乙处7人.答:当m=92时,应调往甲处86人,乙处6人;当m=96时,应调往甲处89人,乙处7人.
(1)设应从乙处调x人去甲处.根据题意得220+x=3(96-x),解得x=17.答:应从乙处调17人去甲处.
(2)设调往甲处y人,甲处现有(220+y)人,则调往乙处(m-y)人,乙处现有(96+m-y)人.根据题意得220+y=3(96+m-y),所以$y=\dfrac{68+3m}{4}.$因为90<m<100,y<m,且m,y均为整数,所以当m=91时$,y=\dfrac{68+3m}{4}=\dfrac{341}{4}($舍去);当m=92时$,y=\dfrac{68+3m}{4}=\dfrac{344}{4}=86;$当m=93时$,y=\dfrac{68+3m}{4}=\dfrac{347}{4}($舍去);当m=94时$,y=\dfrac{68+3m}{4}=\dfrac{350}{4}=\dfrac{175}{2}($舍去);当m=95时$,y=\dfrac{68+3m}{4}=\dfrac{353}{4}($舍去);当m=96时$,y=\dfrac{68+3m}{4}=\dfrac{356}{4}=89;$当m=97时$,y=\dfrac{68+3m}{4}=\dfrac{359}{4}($舍去);当m=98时$,y=\dfrac{68+3m}{4}=\dfrac{362}{4}=\dfrac{181}{2}($舍去);当m=99时$,y=\dfrac{68+3m}{4}=\dfrac{365}{4}($舍去).综上所述,当m=92时,应调往甲处86人,乙处6人;当m=96时,应调往甲处89人,乙处7人.答:当m=92时,应调往甲处86人,乙处6人;当m=96时,应调往甲处89人,乙处7人.
4. 思想方法分类讨论 [难]如图,$A$,$B两地相距90km$,从$A到B的道路依次为60km$平直公路,$10km$上坡公路,$20km$平直公路。甲从$A地开汽车前往B$地,乙从$B地骑摩托车前往A$地。汽车在平直公路上的速度为$120km/h$,上坡的速度为$100km/h$;摩托车在平直公路上的速度为$60km/h$,下坡的速度为$80km/h$,甲、乙两人同时出发。
(1)求甲从$A地到B$地所需要的时间。
(2)求两人出发后经过多少时间相遇。
(3)求甲从$A地前往B$地的过程中,甲、乙经过多少时间相距$10km$。
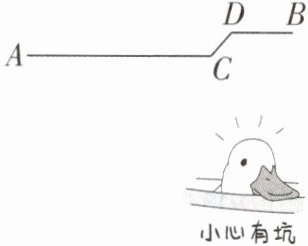
(1)求甲从$A地到B$地所需要的时间。
(2)求两人出发后经过多少时间相遇。
(3)求甲从$A地前往B$地的过程中,甲、乙经过多少时间相距$10km$。

答案:
(1)甲通过AC段所需时间为$t_{1}=\dfrac{60}{120}=0.5(h),$甲通过CD段所需时间为$t_{2}=\dfrac{10}{100}=0.1(h),$甲通过DB段所需时间为$t_{3}=\dfrac{20}{120}=\dfrac{1}{6}(h),$则$t_{1}+t_{2}+t_{3}=0.5+0.1+\dfrac{1}{6}=\dfrac{23}{30}(h),$故甲从A地到B地所需要的时间为$\dfrac{23}{30}h.$
(2)乙通过BD段所需时间为$t_{4}=\dfrac{20}{60}=\dfrac{1}{3}(h),$乙通过DC段所需时间为$t_{5}=\dfrac{10}{80}=\dfrac{1}{8}(h),$则$t_{4}+t_{5}=\dfrac{1}{3}+\dfrac{1}{8}=\dfrac{11}{24}(h)<0.5h,$所以甲、乙会在AC段相遇.设相遇时间为t h,则有$120t+60\left(t-\dfrac{11}{24}\right)=60,$解得$t=\dfrac{35}{72},$故两人出发后经过$\dfrac{35}{72}h$相遇.
(3)设甲、乙经过y h两人相距10km.①当甲在AC段上,乙在CD段上时$,120y+10+20+80\left(y-\dfrac{1}{3}\right)=90,$解得$y=\dfrac{13}{30};②$当甲在CD段上,乙在AC段上时$,60+100\left(y-\dfrac{1}{2}\right)+30+60\left(y-\dfrac{11}{24}\right)=90+10,$解得$y=\dfrac{35}{64}.$故甲从A地前往B地的过程中,甲、乙经过$\dfrac{13}{30}h$和$\dfrac{35}{64}h$相距10km.
(1)甲通过AC段所需时间为$t_{1}=\dfrac{60}{120}=0.5(h),$甲通过CD段所需时间为$t_{2}=\dfrac{10}{100}=0.1(h),$甲通过DB段所需时间为$t_{3}=\dfrac{20}{120}=\dfrac{1}{6}(h),$则$t_{1}+t_{2}+t_{3}=0.5+0.1+\dfrac{1}{6}=\dfrac{23}{30}(h),$故甲从A地到B地所需要的时间为$\dfrac{23}{30}h.$
(2)乙通过BD段所需时间为$t_{4}=\dfrac{20}{60}=\dfrac{1}{3}(h),$乙通过DC段所需时间为$t_{5}=\dfrac{10}{80}=\dfrac{1}{8}(h),$则$t_{4}+t_{5}=\dfrac{1}{3}+\dfrac{1}{8}=\dfrac{11}{24}(h)<0.5h,$所以甲、乙会在AC段相遇.设相遇时间为t h,则有$120t+60\left(t-\dfrac{11}{24}\right)=60,$解得$t=\dfrac{35}{72},$故两人出发后经过$\dfrac{35}{72}h$相遇.
(3)设甲、乙经过y h两人相距10km.①当甲在AC段上,乙在CD段上时$,120y+10+20+80\left(y-\dfrac{1}{3}\right)=90,$解得$y=\dfrac{13}{30};②$当甲在CD段上,乙在AC段上时$,60+100\left(y-\dfrac{1}{2}\right)+30+60\left(y-\dfrac{11}{24}\right)=90+10,$解得$y=\dfrac{35}{64}.$故甲从A地前往B地的过程中,甲、乙经过$\dfrac{13}{30}h$和$\dfrac{35}{64}h$相距10km.
查看更多完整答案,请扫码查看


