《2025年练习部分九年级数学上册沪教版54制》

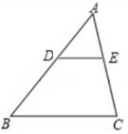
1. 已知点 D,E 分别在$\triangle ABC$的边 AB、AC 上,$AD= 3$厘米,$DB= 4$厘米,$AE= 1.8$厘米,$CE= 2.4$厘米. 那么 DE 与 BC 是否平行？

答案：

解：如图所示
∵AD=3，DB=4，AE=1.8，CE=2.4，
∴$\frac {AD}{AB}=\frac {3}{3+4}=\frac {3}{7}，$
$\frac {AE}{AC}=\frac {1.8}{1.8+2.4}=\frac {3}{7}，$
∴$\frac {AD}{AB}=\frac {AE}{AC}.$
∵∠A=∠A，
∴△ADE∽△ABC，
∴∠ADE=∠ABC，
∴DE//BC.

2. 已知:点 D、E 分别在$\triangle ABC$的边 AB 和 AC 的延长线上,$BD= 2AB$,$CE= 2AC$. 求证:$DE // BC$.

答案： 证明：
∵点D、E分别在△ABC的边AB和AC的延长线上，
BD=2AB，CE=2AC
∴$\frac {AB}{AD}=\frac {AC}{AE}=\frac {1}{3}.$
∵∠A=∠A，
∴△ABC∽△ADE，
∴∠ABC=∠ADE，
∴DE//BC.

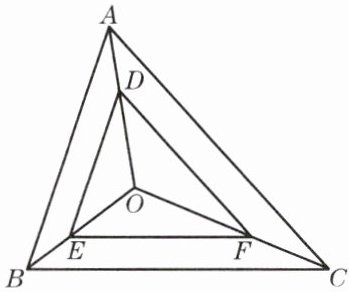
3. 已知:如图,点 O 在$\triangle ABC$内部,点 D、E、F 分别在线段 OA、OB、OC 上,且$DE // AB$,$EF // BC$. 求证:$DF // AC$.

答案： 证明：
∵DE//AB，EF//BC，
∴△ODE∽△OAB，△OEF∽△OBC，
∴$\frac {OD}{OA}=\frac {OE}{OB}，$$\frac {OE}{OB}=\frac {OF}{OC}，$
∴$\frac {OD}{OA}=\frac {OF}{OC}，$
∵∠DOF=∠COA，
∴△DOF∽△AOC，
∴∠OFD=∠OCA，
∴DF//AC．