《2025年练习部分九年级数学上册沪教版54制》

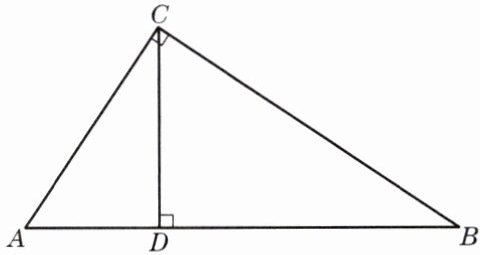
4. 如图,已知△ABC中,∠ACB= 90°,CD⊥AB,垂足为点D,AD= 4,BD= 9.
(1) 求CD的长.
(2) 求cotA、tan∠BCD的值.

答案： 解：
(1)在△ABC中，∠ACB=90°，
∴∠A+∠B=90°.
又
∵CD⊥AB，垂足为点D，
∴∠ADC=∠BDC=90°，
∴∠A+∠ACD=90°，
∴∠ACD=∠B，
∴△ADC∽△CDB.
∴$\frac {AD}{CD}=\frac {CD}{BD}，$
∴$\frac {4}{CD}=\frac {CD}{9}，$
∴CD=6.
$ (2)cotA=\frac {AD}{CD}=\frac {4}{6}=\frac {2}{3}，$
$ tan∠BCD=\frac {BD}{CD}=\frac {9}{6}=\frac {3}{2}.$

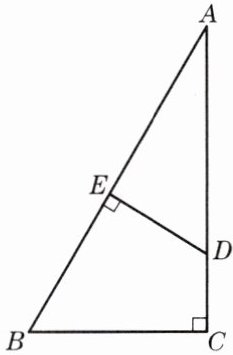
5. 如图,已知△ABC中,∠C= 90°,AC= 3,BC= 2,点D在边AC上,DE⊥AB,垂足为点E,求tan∠ADE的值. 能用两种不同的方法求解吗？

答案： 解：方法一：
∵∠C=90°，DE⊥AB，
∴∠ADE=90°-∠A，∠B=90°-∠A，
∴∠ADE=∠B.
在Rt△ABC中，AC=3，BC=2，
$ tan∠ADE=tan∠B=\frac {AC}{BC}=\frac {3}{2}.$
方法二：
在Rt△ABC中，AC=3，BC=2，
∴$AB=\sqrt{A{C}^2+B{C}^2}=\sqrt{{3}^2+{2}^2}=\sqrt{13}，$
∴$sin∠B=\frac {AC}{AB}=\frac {3}{\sqrt{13}}，$$cos∠B=\frac {BC}{AB}=\frac {2}{\sqrt{13}}，$
∴$tan∠ADE=tan∠B=\frac {sin∠B}{cos∠B}=\frac {\frac {3}{\sqrt{13}}}{\frac {2}{\sqrt{13}}}=\frac {3}{2}.$

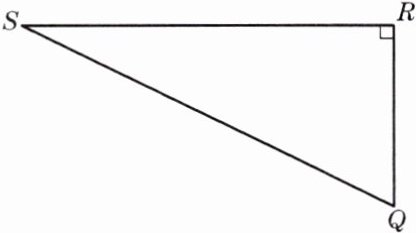
1. 如图,已知△SQR中,∠R= 90°,SR= 2,QR= 1.
(1)求 SQ 的长.
(2)求 sinS、cosS、sinQ、cosQ 的值.

答案： 解：
(1)由勾股定理，得
$ SQ=\sqrt{{SR}^2{+RQ}^2}=\sqrt{{2}^2{+1}^2}=\sqrt{5}.$
$ (2)sinS=\frac {RQ}{SQ}=\frac {1}{\sqrt{5}}=\frac {\sqrt{5}}{5}.$
$ cosS=\frac {SR}{SQ}=\frac {2}{\sqrt{5}}=\frac {2\sqrt{5}}{5}.$
$ sinQ=cosS=\frac {SR}{SQ}=\frac {2}{\sqrt{5}}=\frac {2\sqrt{5}}{5}.$
$ cosQ=sinS=\frac {RQ}{SQ}=\frac {1}{\sqrt{5}}=\frac {\sqrt{5}}{5}.$

2. 如图,已知△ABC中,∠C= 90°,AC= 2,BC= 3. 求 tanA、cotA、sinA、cosA 的值.

答案： 解：
∵∠C=90°，AC=2，BC=3，
∴$AB=\sqrt{A{C}^2+B{C}^2}=\sqrt{13}.$
则$tanA=\frac {BC}{AC}=\frac {3}{2}，$
$ cotA=\frac {AC}{BC}=\frac {2}{3}，$
$ sinA=\frac {BC}{AB}=\frac {3\sqrt{13}}{13}，$
$ cosA=\frac {AC}{AB}=\frac {2\sqrt{13}}{13}.$